El primer gran pensador occidental que es planteja la relació entre les forces i el pensament és el grec Aristòtil. Aristòtil pensava el següent:

1. Per mantenir el moviment d'un cos a la superfície de la Terra, cal que hi actuï una força constant.
2. L'Univers és esfèric i finit i la Terra n'és al centre. La part central està composada per quatre elements: terra, aire, foc i aigua. Cadascun d'aquests elements té un lloc adequat determinat pel seu pes relatiu o "gravetat específica". Cada element es mou, de forma natural, en línia recta —la terra cap avall, el foc cap amunt— cap el lloc que li correspon, a on s'aturarà, per la qual cosa el moviment terrestre sempre és lineal i sempre acaba aturant-se.
3. Els cels, en canvi, es mouen de forma natural i infinita seguint un complex moviment circular, per la qual cosa, deuen estar fets d'un cinquè element, que anomena aither, element superior que no és susceptible de patir cap canvi que no sigui el desplaçament mitjançant un moviment circular.
4. Aristòtil sosté també que els cossos més pesants d'una matèria específica cauen de forma més ràpida que els que son més lleugers quan les seves formes són iguals.

Posteriorment, primer Galileu i a continuació d'altres, especialment Kepler i Newton, utilitzant el mètode científic refuten tots aquests postulats:

1. Llei d'inèrcia: Galileu descobreix que són les forces de fregament (que al cap i a la fi són un tipus de força) les que frenen els cossos a la vida quotidiana, i que en absència de cap força (en particular de les molestes forces de fregament) els cossos tendeixen a moure's a velocitat i amb direcció constants.
2. Galileu demostra que la força de la gravetat produeix la mateixa acceleració a tots els cossos. Ho demostra amb el seu famós experiment: llençant des de la torre de Pisa dues boles de materials diferents i demostrant que arriben en el mateix instant de temps.
3. Kepler, amb les dades experimentals recollides durant molts anys per Tycho Brahe, descobreix que les òrbites dels planetes són elíptiques i que el Sol, centre del sistema Solar, es troba en un dels focus de cada elipse.

 

4. Newton, amb les seves tres lleis del moviment i amb la seva llei de la gravitació universal, demostra que la mateixa llei que explica el pes dels objectes és vàlida per descriure el moviment dels astres, i en particulars les lleis de Kepler. Els astres es mouen per acció de la força de la gravetat. L'Univers obeeix les mateixes lleis que la Terra.

En els seus Principia, l'any 1687, Sir Issac Newton va enunciar les tres lleis del moviment, que són considerades com els axiomes de la Dinàmica.

Tota partícula roman en estat de repòs o de moviment uniforme en línia recta, és a dir, a velocitat constant, a no ser que hi actuï una força.

Si actua una força F sobre una partícula de massa m i com a conseqüència aquesta es mou amb velocitat v aleshores:

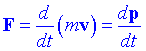
on p = mv s'anomena quantitat de moviment. Si m és independent del temps t aleshores:

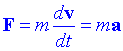
on a és l'acceleració de la partícula. Si sobre una partícula hi actua un conjunt de forces, aleshores es verifica:

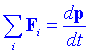
D'això se'n diu principi de superposició de forces.

Si una partícula 1 actua sobre una partícula 2 amb una força F₁₂ en direcció de la línia que uneix les partícules, la partícula 2 actua sobre la partícula 1 amb una força:

En altres paraules, per tota acció existeix una reacció igual.

La segona llei de Newton només es pot considerar completa i precisa quan es defineix la massa m. És possible donar una definició operativa de massa a partir de la tercera llei de Newton. Quan considerem dos cossos aïllats 1 i 2, la tercera llei diu que F₂₁ = -F₁₂. Utilitzant la definició de força donada per la segona llei tindrem:

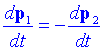
o bé

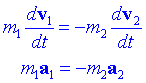
D'aquí en treiem que:

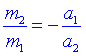
Sempre serà possible establir una massa unitat, per exemple m₁ i determinar la massa de l'altre cos comparant el cocient d'acceleracions quan m₁ hi interactuï. En el sistema internacional la unitat de massa és el Quilogram. La unitat de força és el Newton, que es pot definir com la força necessària per produir una acceleració de 1m/s² a una massa de 1Kg.

Una vegada definida la massa, per poder determinar el moviment dels objectes cal determinar a quina força estan sotmesos. Newton va trobar per exemple l'expressió de la força gravitatòria. La força gravitatòria entre la Terra (de massa M_T i radi R_T) i un objecte qualsevol es pot escriure com:

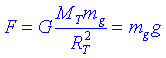
on m_g és la massa gravitatòria de l'objecte. Utilitzant la segona llei de Newton podem escriure:

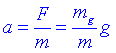
on m s'ha calcular com hem explicat abans. D'aquesta massa m en diem massa inercial. Seria raonable pensar que m_g/m depengués de la composició del material o d'altres variables, d'aquesta manera l'acceleració de caiguda lliure seria diferent per diferents objectes. El fet experimental és que a és la mateixa per tots els cossos, és a dir, que m_g/m sempre val el mateix. Per tant es pren les unitats de G de manera que m_g=m. Els experiments demostren que m_g i m són equivalents amb una precisió de 1 sobre 10¹². La igualtat entre la massa inercial i la massa pesant rep el nom de principi d'equivalència.

Per mesurar el desplaçament dels cossos i aplicar les lleis de Newton cal tenir escollit algun sistema de referència. Els sistemes de referència en què són vàlides les lleis de Newton s'anomenen sistemes de referència inercials. És a dir quan trobem que tot cos lliure de l'acció de cap força es mou en línia recta a velocitat constant (o roman en repòs) el sistema de coordenades utilitzat per estudiar aquest fet serà un sistema de referència inercial.

Quan les lleis de Newton siguin vàlides en un sistema de referència inercial també seran vàlides en qualsevol altre sistema que es mogui a velocitat constant respecte del sistema inercial. Això és degut a que en la segona llei de Newton apareix l'acceleració, és a dir la segona derivada de r respecte del temps, de manera que tot canvi de coordenades en què intervingui una velocitat constant no altera la segona llei. D'això se'n diu principi de relativitat de Galileu.

Per a que en un sistema de referència sigui vàlida la primera llei de Newton, cal que l'espai sigui homogeni i isòtrop. A més, per a que a tots els sistemes inercials les lleis de Newton sigui idèntiques cal que tots aquests sistemes tinguin el mateix temps t. És a dir, en la dinàmica Newtoniana, el temps és una magnitud absoluta independent del sistema de referència.

Si una força actua sobre una determinada massa m, es produeix una determinada variació del moment lineal que anomenem impuls I. Aquesta variació es pot calcular integrant la força respecte del temps:

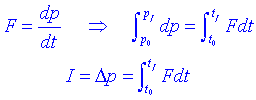
El promig temporal d'una força durant un temps D t es pot escriure com:

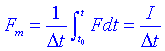
Aquesta expressió pot ser útil per exemple per calcular la força de retrocés d'una metralladora que dispara R projectils per segon, de massa m i a velocitat v. La força vindrà donada per:

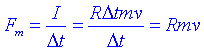
Si no tenim cap força, F=0, la segona llei de Newton ens diu que:

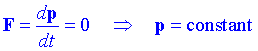
Per tant, si la força que actua sobre una partícula és zero, el seu moment es conserva.

Considerem ara dues partícules en lloc d'una. A més suposem que les úniques forces que actuen sobre les partícules són forces d'interacció entre elles mateixes. Utilitzant la segona i tercera lleis de Newton podem escriure:

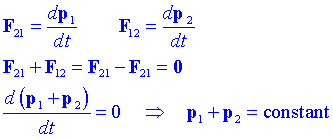
Aquest resultat l'anomenem llei de conservació de la quantitat de moviment i és fàcilment generalitzable a n partícules fent el mateix raonament.

Suposem que dues masses m₁ i m₂ que es mouen sobre la mateixa recta xoquen. Anem a determinar les velocitats després del xoc v₁' i v₂' en funció de les velocitats inicials v₁ i v₂.

El moment abans del xoc serà:

Per analitzar que passa durant el xoc és molt convenient situar-se sobre un sistema inercial en el que p=0. Suposem que ens situem sobre un sistema que es mou a una velocitat:

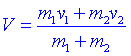
respecte a aquest nou sistema de referència les velocitats de les dues masses es poden escriure:

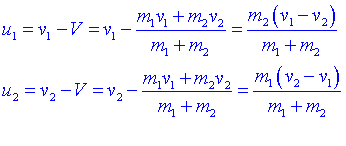
Es comprova fàcilment que respecte d'aquest sistema de referència el moment és nul:

En el moment del xoc, si el moment s'ha de conservar, passi el que passi, fixem-nos que l'única possibilitat és que:

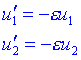
on e és l'anomenat coeficient de restitució. Es pot avaluar experimentalment i pren valors entre 0 i 1. Si e =1 diem que el xoc és elàstic (les masses conserven les seves velocitats) i si e =0 diem que el xoc és totalment inelàstic (les masses queden unides i en repòs).

Si tornem al sistema de referència inicial trobarem les velocitats:

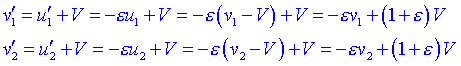
Substituint el valor de V trobem que:

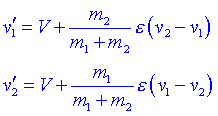
Per un xoc totalment inelàstic e =0 tindrem:

Per un xoc elàstic e =1:

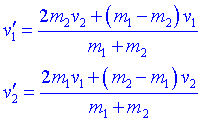
Aquí podem considerar uns quants casos particulars:

1. Si m₁=m₂ i v₂=0 aleshores:



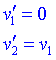
és a dir, si dues masses iguals xoquen, i una és estacionària, aleshores s'intercanvien els moments.

2. Si m₁<<m₂ i v₂=0 aleshores:



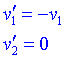
és a dir, que si una partícula de massa petita impacta contra una massa molt gran, la partícula "rebota".

3. Si m₁=m₂:

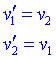
Si les masses són iguals les partícules simplement intercanvien les seves velocitats.

Un coet és un dispositiu que basa la seva propulsió en l'expulsió d'una determinada quantitat de massa per unitat de temps i a una determinada velocitat que anomenarem u i prendrem u>0. Considerem que li passa al coet durant un cert D t. El coet incrementa la seva velocitat v i perd massa D m<0. Per tant:

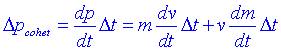
Considerem ara que està passant amb els gasos. Els gasos surten expulsats a velocitat (u-v) en un cert D t:

Fixem-nos que el signe de D p_gas és el correcte. Si hi ha una força externa, la suma de moments ens haurà de donar:

Substituint i fent el límit obtindrem l'equació diferencial que ens descriu el moviment:

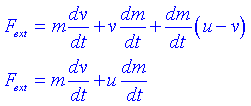
Anem a considerar un cas particular senzill, quan F_ext=0. Si fem F_ext=0 obtenim l'equació:

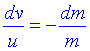
Integrant l'equació obtenim:

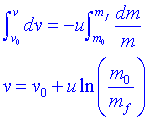
Fixem-nos que serà molt important assegurar que u sigui el més gran possible. Si el coet té una càrrega útil del 10%, tindrem que:

Considerem un massa m que penja d'un fil de massa menyspreable i longitud l. El pèndol es troba sota l'efecte de la força de la gravetat. Anem a deduir les equacions del moviment per desplaçaments petits respecte de la posició d'equilibri:

Si l'angle q és molt petit, aleshores Això voldrà dir que només són apreciables moviments horitzontals, però els verticals són menyspreables. Per tant, aleshores: T=g i F_y=0. En la direcció x podrem escriure la segona llei de Newton:

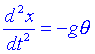
Es convenient escriure x en termes de l'angle: Substituint a l'equació diferencial:

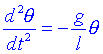
Fixem-nos que la massa no apareix en aquesta equació. El moviment d'un pèndol no depèn de la seva massa. Aquest fet ja va ser descobert per Galileo, i és la base per a l'exactitud dels rellotges de pèndol que es desenvoluparien en una època posterior. L'equació anterior, per inspecció es veu que la solució és pot escriure com:

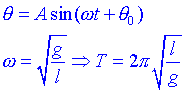
Fixem-nos, doncs que mesurant el període d'un pèndol de longitud coneguda es pot mesurar g. Com més llarga és la corda més llarg és el període del pèndol. Si anem a la Lluna i fem anar un pèndol veurem que oscil·la més a poc a poc que a la Terra.

La força d'una molla depèn del seu estirament. Si imaginem la molla situada sobre un eix X, la força de la molla en funció del seu allargament x es pot escriure com:

on la k s'anomena constant recuperadora. D'aquesta expressió s'anomena llei de Hook. El fet que l'allargament sigui proporcional a la força fa que sigui senzill construir mecanismes per a la mesura de forces (ex. dinamòmetre). Si lliguem una massa m a l'extrem d'una molla, utilitzant la segona llei de Newton deduïm que l'equació del moviment serà:

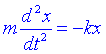
Qualsevol sistema que obeeixi una equació d'aquestes característiques s'anomena Oscil·lador Harmònic. Per inspecció veiem que la solució d'aquesta equació és:

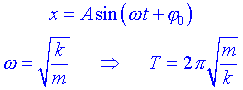
El període d'oscil·lació s'incrementa amb la massa i disminueix amb k. Les forces entre les molècules de molts sòlids es poden escriure en primera aproximació d'igual manera que la llei de Hook. Per tant en Física l'estudi d'aquest tipus de moviment és important.

Quan un objecte es mou a través d'un fluid com ara l'aire o l'aigua, està sotmès a forces de retard o arrossegament que tendeixen a disminuir la velocitat de l'objecte. Aquestes forces són aproximadament proporcionals a la velocitat per velocitats petites i proporcionals al quadrat de la velocitat per velocitats grans. Anem a veure com deduir les equacions del moviment en aquestes condicions.

Suposem que tenim un vaixell a l'aigua i que els motors propulsen el vaixell amb una certa força constant F. En aquestes condicions la força d'arrossegament de l'aigua serà lineal amb la velocitat. Volem trobar la velocitat del vaixell a partir del moment en què es connecten els motors, i sortint del repòs. La segona llei de Newton diu que hem d'escriure:

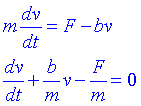
on b és un paràmetre que depèn de la forma del vaixell, viscositat de l'aigua, etc. La solució d'aquesta equació tindrà la forma:

Substituint trobarem que:

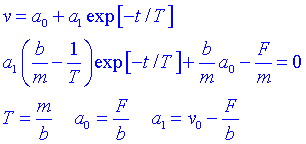
Observem que la solució és una constant més una exponencial decreixent amb el temps. Per tant, conforme passa el temps, la velocitat s'apropa a una velocitat màxima F/b. Aquesta velocitat rep el nom de velocitat límit.

Suposem ara que un paracaigudista es llença des d'un avió i volem calcular com canvia la velocitat amb el temps. En aquestes condicions la força d'arrossegament és proporcional al quadrat de la velocitat:

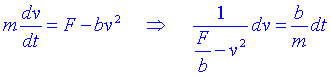
Integrant:

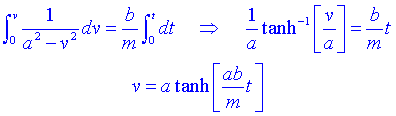
Retornant a la constant a el seu valor:

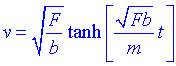
Conforme el temps creix, la tangent hiperbòlica tendeix a 1. Per tant la velocitat creix fins arribar a una velocitat límit que ve donada per:

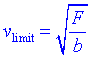
Per a un paracaigudista en caiguda lliure aquesta velocitat és d'uns 200Km/h.

Si intentem desplaçar un cos damunt d'un altre (exemple: un armari sobre el terra) apareixen forces degudes al contacte entre les superfícies dels dos cossos. Aquestes forces s'oposen al moviment i s'anomenen forces de fregament. Les forces de fregament presenten un seguit de propietats interessants:

1. Són, en primera aproximació, independents de la superfície de contacte entre els dos cossos.
2. Són proporcionals a la força normal entre les dues superfícies: F = m N on m s'anomena coeficient de fregament.
3. El coeficient de fregament és diferent segons el cos estigui en repòs o en moviment. Distingim, doncs entre el coeficient de fregament estàtic m _e i el coeficient de fregament dinàmic m _c. Les forces de fregament estàtiques són les que fan, per exemple, que sigui possible mantenir estacionari un cos sobre un pla inclinat.
4. Sempre es verifica que m _e > m _c.
5. En general m _c depèn de la velocitat, però per velocitats petites, entre 1cm/s a uns quants metres per segon, m _c és aproximadament constant.
6. El valor de m depèn de les superfícies de contacte.

Una manera de mesurar m _e i m _c consisteix a situar un objecte sobre un pla inclinat amb un angle inicial q =0. Si comencem a augmentar l'angle, arribarà un moment en què el cos començarà a caure. Sigui aquest angle crític q _c i calculem-ne el valor de m _e. Si prenem l'eix X paral·lel al pla inclinat i l'eix perpendicular, podrem escriure:

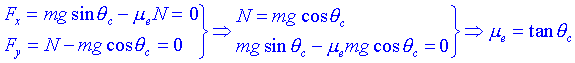
Per angles superiors, el cos baixa pel pla. Anem a calcular-ne l'acceleració:

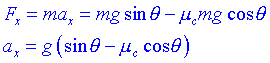
Mesurant a_x és possible deduir-ne el valor de m _c.

Anem a veure com s'ha de modificar la segona llei de Newton en el cas de que vulguem utilitzar-la en un sistema no inercial. Suposem que en un sistema fix F s'observa un mòbil el moviment del qual ve descrit pel vector de posició r_F. Un altre sistema de referència, l'origen del qual es troba a l'extrem del vector R_o observa també el mòbil amb les seves pròpies coordenades i la posició vindrà donada pel vector r_M. La relació entre els tres vectors vindrà donada per:

Derivant respecte del temps trobarem la relació entre les velocitats i les acceleracions mesurades en tots dos sistemes:

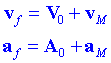
Si multipliquem per la massa trobem que:

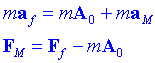
Per tant, en el sistema no inercial, s'observen les mateixes forces que en el sistema fix més una força anomenada fictícia provocada pel terme -mA₀. Aquest terme provoca una força en direcció contrària a l'acceleració del sistema no inercial i és sempre proporcional a la massa.

Exemples:

Si un cotxe frena, tenim una acceleració negativa en la direcció de l'eix negatiu de les X. Per tant els ocupants noten una força que els empeny cap endavant.

Si un cotxe gira, l'acceleració és en direcció al centre de curvatura (acceleració centrípeta). Per tant els ocupants notaran una força en direcció contrària, anomenada força centrífuga:

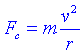
La força centrífuga, com les altres forces fictícies, és proporcional a la massa i creix ràpidament amb la segona potència de la velocitat. Aquest fet s'aprofita en un aparell anomenat centrífuga que s'utilitza per a la separació de substàncies (preferentment líquids i sòlids).