L’existència d’espècies poliatòmiques estables, ja siguin elementals o compostes, implica que els àtoms poden interactuar entre si per formar agregats que tenen una energia més baixa que els fragments separats. Quan aquesta disminució de l’energia excedeix 10kcal/mol d’àtoms aproximadament, diem que existeixen enllaços químics doncs es produeixen espècies que tenen propietats químiques definides i característiques. Una reacció química és un procés que canvia un cert ordenament d’enllaços per un altre.

No només la pròpia formació de l’enllaç s’explica en termes energètics, si no que totes les seves característiques: tipus d’enllaç, longitud d’enllaç i angles d’enllaç s’explica en termes de disposicions de mínima energia.

Cada àtom posseeix una determinada configuració electrònica, que s’especifica indicant quins orbitals atòmics ocupen els electrons. Els electrons de la capa més externa tenen energies més grans i reben el nom d’electrons de valència. Els electrons de la capa de valència són els que intervenen en la formació de l’enllaç entre dos o més àtoms i per tant són els que en determinen les propietats químiques.

Quan dos àtoms s’apropen, resulta que la configuració de mínima energia deixa de ser la configuració electrònica que cada àtom presentava per separat. Els electrons de valència, que són els electrons més externs i més dèbilment lligats presenten energies relativament grans. Aquests electrons poden reduir la seva energia passant a ocupar uns nous orbitals, els orbitals moleculars que donen lloc a la formació del que s’anomena enllaç covalent.

Hi ha vàries descripcions possibles de l’enllaç covalent. La més senzilla de totes és l’anomenada teoria de l’enllaç de valència. En aquest model, els orbitals moleculars es formen per la superposició (suma) de dos orbitals de valència de dos àtoms. Això implica una acumulació de densitat electrònica entre dos nuclis. Aquest fet és d’una importància fonamental. L’energia potencial del sistema és més baixa quan els electrons són molt a prop de qualsevol dels dos nuclis o quan són en una regió que està relativament a prop dels dos nuclis alhora. Per tant l’ocupació d’orbitals moleculars per dos electrons permet disminuir l’energia total de la molècula, i per tant, es forma un enllaç. És en aquest sentit doncs que és possible afirmar que un enllaç suposa la compartició d’una parella d’electrons per dos nuclis.

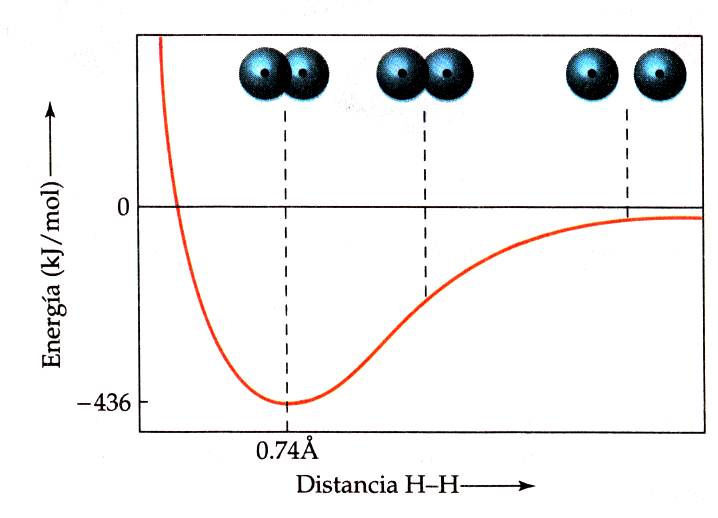
Sempre hi ha una distància òptima entre els dos nuclis enllaçats en qualsevol enllaç covalent. A mesura que els àtoms s’apropen augmenta la superposició, augmenta la densitat electrònica entre els nuclis i l’energia disminueix fins a un cert mínim que anomenem energia d’enllaç. La distància internuclear en la que l’energia és mínima representa la longitud d’enllaç. Si els nuclis s’apropen més apareixen forces de repulsió electrostàtiques que fan que l’energia pugi ràpidament. Així doncs, la longitud d’enllaç correspon a un equilibri entre forces d’atracció entre càrregues diferents (electrons i nuclis) i forces de repulsió entre càrregues iguals (electró-electró i nucli-nucli).

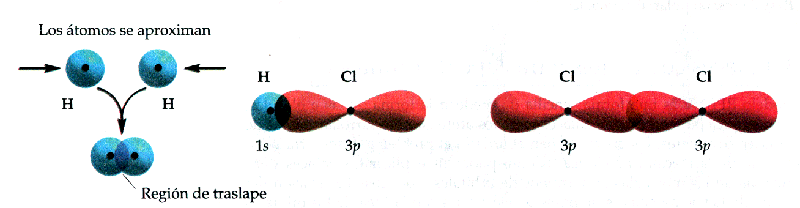
Anem a veure algun exemple. En la figura podem veure la formació de la molècula d’hidrogen. Al superposar-se els orbitals, la densitat electrònica es concentra entre els nuclis. Com que ambdós electrons són atrets simultàniament pels nuclis, mantenen units als àtoms i es forma un enllaç covalent. Un altre exemple pot ser la molècula HCl. Tots els orbitals de valència del clor estan plens amb excepció de l’orbital 3p que conté un sol electró. Aquest electró s’aparella amb l’únic electró de l’hidrogen per formar l’enllaç. A la figura es pot veure la superposició de l’orbital 1s de l’hidrogen amb el 3p del clor. Anàlogament es pot descriure la molècula de clor com a superposició dels orbitals 3p de tots dos àtoms.

El model més senzill que explica la geometria de les molècules és el model de Repulsió del Parell Electrònic del Nivell de València (RPENV). Hem vist en les molècules diatòmiques que els àtoms s’uneixen entre si compartint parells d’electrons del nivell de valència. En una molècula els parells d’electrons es repel·leixen entre si. Per tant la geometria d’una molècula correspondrà a la que minimitzi la repulsió entre els parells d’electrons, és a dir, la geometria d’una molècula correspondrà a la que permeti minimitzar l’energia potencial dels electrons i per tant de la molècula. Per tant depenent del nombre de parells d’electrons les molècules adoptaran geometries diferents tal i com veiem a la figura.

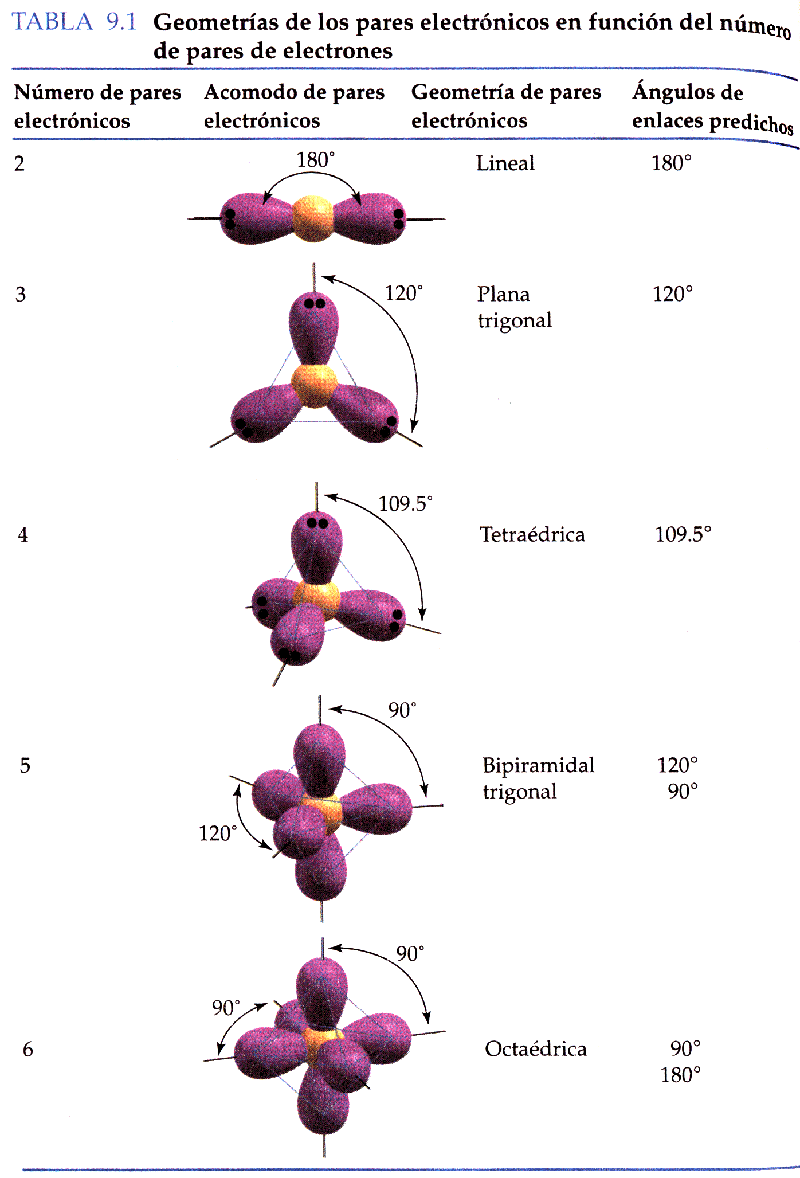
Quan en una molècula hi ha parells d’electrons no enllaçants o enllaços múltiples s’observen petites desviacions en els angles d’enllaç que hem comentat abans. Els parells d’electrons enllaçants són atrets pels dos nuclis dels àtoms enllaçats. En canvi, l’única influència sobre el moviment dels electrons no enllaçants és l’atracció d’un sol nucli i per tant ocupen una extensió major en l’espai. El resultat és que els parells d’electrons no enllaçants exerceixen forces de repulsió més intenses sobre els parells d’electrons adjacents i per aquest motiu tendeixen a comprimir els angles que hi ha entre els parells enllaçants, de manera que l’energia sigui mínima.

Anem ara a veure com es construeixen els orbitals d’enllaç a partir dels orbitals atòmics per tal de poder explicar la geometria de les molècules. Per a aquest motiu cal introduir el concepte d’orbital híbrid. Un orbital atòmic híbrid és el resultat d’una combinació lineal de dos o més orbitals atòmics.

Híbrids sp. Geometria Lineal: Si es suma un orbital s i un p resulta una nova funció híbrida. Si restem obtenim una segona funció híbrida. Aquestes funcions híbrides s’anomenen orbitals híbrids sp i són equivalents llevat en un gir de 180º. Amb aquests orbitals és fàcil d’explicar l’enllaç de molècules lineals, tipus HgCl₂, BeF₂

Híbrids sp². Geometria Trigonal Plana: Hi ha tres maneres possibles de combinar un orbital s i dos orbitals p per produir tres orbitals híbrids equivalents sp². Els tres orbitals híbrids són idèntics en tot llevat de l’orientació, doncs presenten un gir de 120º entre ells. Amb aquests orbitals es descriuen molècules amb geometria trigonal plana, com ara BF₃, BCl₃, B(CH)₃.

Híbrids sp³. Geometria Tetraèdrica: Hi ha quatre maneres independents de combinar un orbital s amb tres orbitals p per produir 4 nous orbitals híbrids equivalents sp³. Cada orbital híbrid sp³ es dirigeix cap al vèrtex d’un tetraedre regular. Aquests híbrids permeten descriure molècules com ara CH₃Cl, CF₄, CH₄, NH₄⁺, BH₄^-.

Híbrids dsp³. Geometria Bipiramidal Trigonal. La combinació d’un orbital un orbital s i tres orbitals p dona lloc a un conjunt de tres orbitals híbrids equivalents situats en un pla equatorial formant angles de 120º i dos orbitals híbrids més allargats perpendiculars als orbitals equatorials. Aquesta hibridació permet descriure geometries bipiramidals trigonals com les de les molècules PCl₅.

Híbrids d²sp³. Geometria Octaèdrica: La combinació de dos orbitals d, un s i tres p dona lloc a 6 orbitals híbrids equivalents dirigits cap al vèrtex d’un octaedre regular. Permet descriure molècules com ara el SF₆.

Els orbitals híbrids estan formats per lòbuls que s’estenen a major distància del nucli que els propis orbitals atòmics a partir dels quals es formen. Això fa que siguin capaços de superposar-se amb orbitals d’altres àtoms de manera molt més efectiva. Per tant els enllaços formats per orbitals híbrids tindran energies més baixes, és a dir, seran més forts que els enllaços formats per simples orbitals atòmics.

Per descriure la polaritat de l’enllaç és necessari treballar amb un tractament més rigorós de l’enllaç covalent. És possible aconseguir una descripció matemàtica relativament senzilla i aproximada considerant que els Orbitals Moleculars es poden escriure com Combinació Lineal d’Orbitals Atòmics. Això significa que per obtenir la funció d’ona d’un orbital molecular es considera la combinació lineal (sumant o restant) de la funció d’ona de l’orbital atòmic d’un àtom a amb la funció d’ona de l’orbital atòmic d’un altre àtom b. Comencem suposant que els dos àtoms són d’hidrogen:

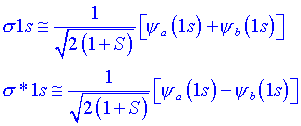
Els factors són factors de normalització; S és la integral de superposició:

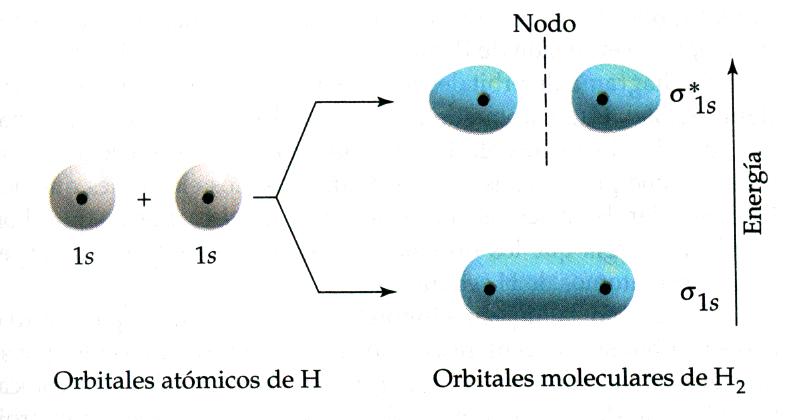
Quan es sumen les dos funcions 1s, es reforcen en tot lloc, però més notablement en la regió compresa entre els dos nuclis, cosa que contribueix a minimitzar l’energia potencial coulòmbica. Per tant aquest orbital té caràcter enllaçant i es denota per s 1s. Quan es resten, apareix un pla nodal entre els dos nuclis i la funció ondulatòria és de signe oposat a les dues bandes del pla. A la regió internuclear es produeix un dèficit de probabilitat que contribueix a elevar l’energia potencial del sistema i el node produeix un augment de l’energia cinètica de l’electró. En conseqüència l’energia total és elevada i per tant l’orbital resultant és antienllaçant. Aquest orbital es denota com s *1s.

Resumint, la combinació lineal de dos orbitals atòmics produirà dos orbitals moleculars, un d’energia més alta i un d’energia més baixa que la dels orbitals atòmics. Si l’orbital molecular té un node entre els nuclis serà antienllaçant i si hi ha un augment de la densitat de probabilitat entre els nuclis l’orbital serà enllaçant.

Anàlogament es pot considerar la combinació lineal d’altres orbitals atòmics. Per exemple, en les molècules diatòmiques homonuclears del segon període, els orbitals 1s d’aquests àtoms són molt propers al nucli, tenen una energia molt baixa i per tant amb prou feines són afectats pel fet que l’àtom estigui lliure o enllaçat químicament. Per tant aquests electrons es consideren no enllaçants. Cal aleshores considerar els orbitals moleculars que s’obtenen a partir de la combinació lineal d’orbitals 2s i 2p.

Per establir les aproximacions de la CLOA hem fet combinacions lineals d’orbitals atòmics del mateix tipus, per poder conservar la simetria de la molècula. Els orbitals moleculars de les molècules heteronuclears no són simètrics. Si la molècula diatòmica està formada per àtoms de nombres atòmics similars, com ara el CO, NO i CN, la asimetria no és pronunciada i es pot descriure satisfactòriament l’estructura electrònica en termes d’orbitals moleculars semblants als que s’utilitzen per descriure les molècules diatòmiques homonuclears.

Considerem la molècula de BN. Podem formar orbitals s 2s i s *2s a partir dels orbitals 2s dels dos àtoms. Com que el nitrogen té més càrrega nuclear, l’orbital atòmic 2s d’aquest nucli és de menor energia que l’orbital 2s del nucli de bor. En conseqüència, esperem que l’orbital de més baixa energia, o orbital enllaçant s format per aquesta combinació estarà principalment concentrat prop de l’àtom de nitrogen, ja que aquesta és la regió de més baixa energia potencial. Aquesta asimetria es pot produir sumant els orbitals amb els coeficients adequats:

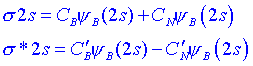
on C_N > C_B. El corresponent orbital antienllaçant ha de tenir un node entre els nuclis i ser de més alta energia, per tant esperem que l’orbital antienllaçant estigui concentrat prop del nucli de bor majoritàriament. Per tant C’_B > C’_N. Amb la resta d’orbitals moleculars ocorre el mateix.

Quan la diferència entre els nombres atòmics és gran els orbitals moleculars es formen per la combinació dels orbitals d’energia similar. Un exemple és la molècula de HF. L’energia de l’orbital 1s de l’hidrogen i l’energia dels orbitals 2p del fluor són prou similars i donen lloc a un parell d’orbitals enllaçant-antienllaçant. Els orbitals 2p_x i 2p_y del fluor queden com orbitals atòmics no enllaçants. Com l’orbital 2p del fluor té una energia inferior al 1s de l’hidrogen, s’espera que el parell d’electrons de l’orbital enllaçant s de HF estigui més temps prop del nucli de fluor i que en conseqüència la molècula del HF ha de ser polar, tal i com s’observa.

Un exemple de compartició extremadament desigual és la molècula gasosa de florur de liti LiF. En aquest cas es genera un parell d’orbitals s -s * a partir de l’orbital 2s del Li i un orbital 2p del fluor. Com que l’energia de l’orbital 2p és molt inferior a la del 2s el parell d’electrons de l’orbital enllaçant roman quasi tot el temps prop de l’àtom de fluor. Com que el LiF és una molècula tan polar es diu que l’enllaç és iònic,, i que el Liti ha cedit un electró al fluor. L’enllaç iònic s’entén, doncs com un cas extrem de l’enllaç covalent polar.

Per tant, el fet que els electrons tendeixin a distribuir-se al voltant de les zones on l’energia potencial és mínima, fa que els enllaços heteronuclears siguin en major o menor mesura enllaços covalents polars. En l’apartat següent s’estableix una magnitud anomenada electronegativitat que ens permetrà predir qualitativament la polaritat dels enllaços.

Es diu que un element és electronegatiu quan en les seves interaccions químiques té més tendència a adquirir electrons que a perdre'ls. L’electronegativitat descriu, doncs l’atracció que exerceix un àtom sobre els electrons d’enllaç. S'han fet diversos intents per crear una escala quantitativa d'electronegativitat.

El procediment més senzill potser fos el de R.S.Mulliken, que suggerí que l'electronegativitat és proporcional al promig de l'energia d'ionització i l'afinitat electrònica.

La més usual és la de Pauling. Pauling va obtenir valors d’electronegativitat comparant l’energia d’enllaç entre àtoms desiguals, AB, amb les energies mitjanes dels enllaços de A₂ i B₂. Si, per exemple, HF formés un enllaç covalent, seria d’esperar que l’energia d’enllaç HF fos pròxima al promig (mitjana aritmètica o geomètrica) de les energies d’enllaç de H₂ i F₂. El que passa, però, és que en molècules com HF els enllaços són més forts que els predits a partir dels promitjos. L’energia d’enllaç del HF és de 565kJ/mol, mentre que les energies d’enllaç de H₂ i F₂ són 432 i 139 kJ/mol, respectivament. La mitjana geomètrica és de 245kJ/mol, que és molt menor que l’energia d’enllaç observada en el HF. Aquesta energia d’enllaç extra D d’una molècula AB se suposa que és una conseqüència del caràcter iònic parcial de l’enllaç, deguda a la diferència d’electronegativitats entre els dos elements. La diferència d’electronegativitats entre els àtoms A i B es pot definir com:

on D_AB, D_AA i D_BB són les energies d'enllaç de les molècules diatòmiques corresponents. La rel quadrada s’utilitza perquè proporciona un conjunt de valors d’electronegativitat més consistent. Com que en aquesta equació només s’obtenen diferències, s’ha d’assignar a un àtom un valor específic d’electronegativitat i aleshores es poden calcular fàcilment els valors per als altres àtoms. Al fluor, l’element més electronegatiu se li assigna un valor de 3,98.

L’electronegativitat és una mesura de l’atracció que exerceix un àtom pels electrons d’enllaç que ha format amb un altra àtom. Els electrons d’enllaç de la molècula HF són arrossegats cap a l’àtom F, degut a la seva major electronegativitat. L’enllaç HF té caràcter iònic parcial. La diferència de les electronegativitats dels elements que formen part d'una molècula té relació directa doncs amb els moments dipolars, el tipus d'enllaç i l'energia d'enllaç.

Una diferència de més de 2,0 dona com a resultat un enllaç que es pot considerar iònic; una diferència en l’interval 0,4-2,0 dona com a resultat un enllaç covalent amb caràcter iònic o enllaç covalent polar. Una diferència menor de 0,4 dóna com a resultat un enllaç que pot ser considerat com a covalent.

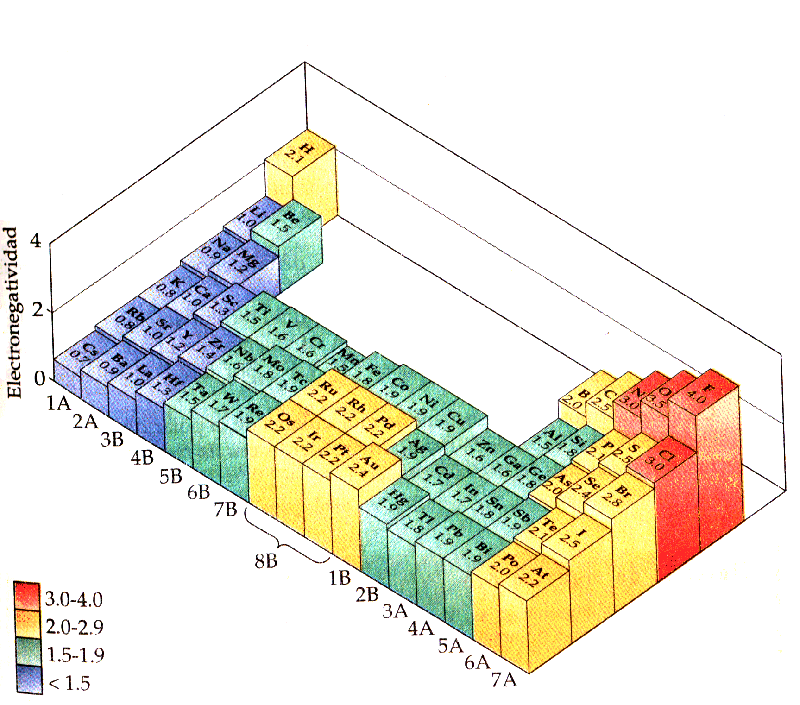
Veient aquesta taula s'observa que l'aptitud per atreure i mantenir electrons augmenta d'esquerra a dreta al llarg de qualsevol fila i de la part inferior a la superior en qualsevol columna de la taula periòdica. Això és consistent amb les tendències de l’energia d’ionització i de l’afinitat electrònica.

L’enllaç iònic es produeix quan hi ha una transferència d’electrons entre àtoms o molècules, resultant-ne espècies químiques amb càrrega elèctrica ben definida que s’anomenen ions i que quedaran unides per interacció electrostàtica. Per tant estarem parlant d’un tipus d’enllaç fort i adireccional. Les forces electrostàtiques obliguen als ions a formar estructures que maximitzin les forces d’atracció i minimitzin les forces de repulsió, és a dir, a formar estructures que minimitzin l’energia potencial electrostàtica. Aquestes estructures són altament ordenades i corresponen a ordenaments geomètrics infinits anomenats cristalls.

En el model de l’enllaç iònic imaginem les partícules enllaçades com si fossin entitats esfèriques que tenen una càrrega neta positiva o negativa. Una distribució esfèrica de càrrega es comporta com si la càrrega neta estigués concentrada en al centre de l’esfera. Per tant la major simplificació del model de l’enllaç iònic és que podem calcular les forces electrostàtiques que actuen entre els ions utilitzant la llei de Coulomb, com si els ions fossin càrregues puntuals. Aquest enfoc no és exacte (però permet calcular correctament els ordres de magnitud) i haurà de ser refinat.

Les estructures dels sòlids cristal·lins són aquelles que permeten el contacte més íntim entre els ions, per tal de maximitzar les forces d’atracció i aconseguir la mínima energia possible. Per tant resulta interessant considerar la manera en què esferes de la mateixa grandària es poden disposar de la manera més eficient possible, és a dir, deixant el mínim espai lliure possible. Hi ha dues maneres, anomenades empaquetament hexagonal compacte i empaquetament cúbic compacte. En aquests empaquetaments existeixen tres tipus d’espais buits anomenats llocs triangulars, els llocs tetraèdrics i els llocs octaèdrics, depenent del nombre i disposició de les esferes al voltant dels espais buits. Les estructures cristal·lines de molts compostos binaris dels tipus AB, AB₂ i A₂B estan relacionades de manera senzilla amb les estructures d’empaquetament compacte. Amb molta freqüència, l’ió B es pot representar mitjançant esferes amb una estructura d’empaquetament compacte mentre que l’ió A ocupa els intersticis o espais buits entre les esferes de B.

La relació de radis entre els ions A i B determina, no la grandària màxima que s’ha d’establir per a que els ions més petits càpiguen en els llocs buits, si no que determina a partir de quin radi s’hi col·loquen. Això és així en la majoria dels casos, perquè d’aquesta manera els ions grans amb càrregues idèntiques s’han de separar (disminuint les repulsions) per permetre la cabuda dels ions petits. D’altra banda l’apropament entre els ions de diferent càrrega és màxim (maximitzant les forces d’atracció). La relació entre els radis dels ions, doncs determina el nombre màxim de coordinació o nombre de veïns immediats que poden agrupar-se al voltant d’un ió central per tal d’aconseguir que l’energia del cristall sigui mínima.

Comencem amb la reacció de formació del NaCl cristal·lí a partir dels elements:

Aquest és un procés molt complex. Fixem-nos en el següent gràfic:

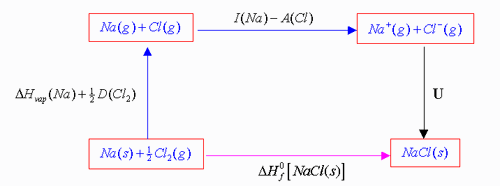
El canvi d’entalpia per la ruta directa és el calor de formació del NaCl(s):

Veiem que el procés de formació es pot desglossar en tres etapes:

1. El primer pas consisteix en la vaporització del sodi metàl·lic i la dissociació del clor en àtoms. Per tant aquest primer pas mostra com l’estabilitat del sodi metàl·lic i de les molècules de clor afecten l’energia alliberada per la reacció total.



2. En el segon pas, es converteixen els àtoms del gas en ions. Per fer això es necessita que posem en el sistema una quantitat d’energia igual a l’energia d’ionització del sodi menys l’afinitat electrònica del clor.



3. En el tercer pas, els ions es condensen a la xarxa cristal·lina. L’energia alliberada pel sistema en aquest pas s’anomena energia iònica de la xarxa cristal·lina i és una mesura directa de l’estabilitat del cristall. De fet es defineix l’energia iònica de la xarxa com l’energia necessària per separar totalment el compost iònic en els ions gasosos:

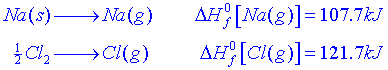
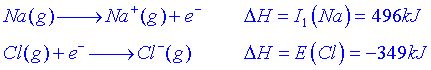
L’energia de la xarxa no es pot calcular directament, però és possible utilitzar la llei de Hess per sumar cada pas de tal manera que obtinguem l’energia de la xarxa; al fer això estem construint el que s’anomena com un cicle Born-Haber.

La suma de tots els passos del camí indirecte ha de ser equivalent al camí directe i per tant:

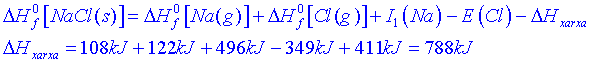
O sigui que l’energia de la xarxa del clorur de sodi és de 788 kJ/mol.

Examinarem ara la formació del clorur de sodi a partir dels àtoms en estat gasós. D’aquesta manera ens centrarem únicament en els factors energètics que influeixen en la formació de l’enllaç iònic: no ens haurem de preocupar per l’enllaç del sodi metàl·lic o del clor molecular. Imaginarem aleshores que el cristall es forma en tres etapes: la primera la formació dels ions gasosos a partir dels àtoms; la segona la formació de molècules diatòmiques gasoses a partir dels ions, i tercera la formació del cristall iònic.

En el primer pas, cal subministrar 118kcal/mol als àtoms de sodi per a ionitzar-los, mentre que els àtoms de clor desprenen 83,4 kcal/mol en absorbir un electró. Per tant per formar els ions a partir dels àtoms calen 35kcal/mol de parells iònics. Per tant, si el sodi i el clor l’única cosa que fan és formar octets complerts es requereix energia. Així doncs els àtoms no tenen cap impuls natural a arribar a una estructura d’octets. Cal una altra raó per a justificar la formació de l’enllaç.

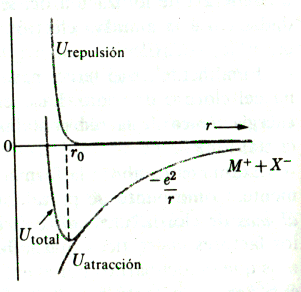
Ara considerem la formació de la molècula gasosa a partir dels ions. L’energia potencial disminueix conforme els ions s’apropen. Quan els dos ions són molt a prop, els electrons exteriors comencen a ocupar el mateix espai i es desenvolupa una potent força de repulsió, que es tradueix en un augment de l’energia potencial. La distància r₀ a la qual l’energia potencial és mínima és la distància d’enllaç. Per la forma de la corba de l’energia potencial podem veure que l’energia potencial a r₀ és quasi igual a la contribució deguda a l’atracció únicament. Experimentalment s’ha trobat que r₀=2,38� . L’energia d’enllaç és molt aproximadament de –139,3kcal/mol (-q²/4p e ₀r₀ ). Així doncs, l’energia que s’allibera quan es formen aquestes molècules a partir dels àtoms gasosos és de 35,0-139,3 = -104,3 kcal/mol. Per tant l’energia del sodi i del clor iònicament enllaçats és més baixa que la dels àtoms separats. Per tant, l’energia necessària per formar els ions és més que compensada per l’energia deguda a l’atracció coulòmbica.

Anem ara a centrar-nos en la formació del cristall iònic. Per fer-ho senzill, calcularem primer l’energia d’un ió sodi d’un cristall unidimensional, és a dir una filera on s’alternen ions clor i ions sodi separats per una distància r₀.

Aleshores:

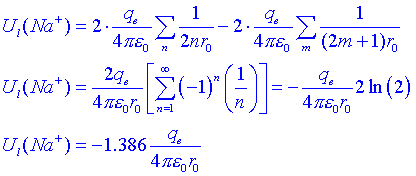
Per tant, fixem-nos que l’energia de l’ió sodi és més baixa en aquest cristall unidimensional que en la molècula diatòmica. De manera semblant podríem seguir sumant totes les altres fileres que tindríem en un cristall tridimensional real. Per a qualsevol xarxa cristal·lina, l’energia es pot escriure com:

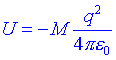
on M s’anomena constant de Madelung. Per una xarxa cúbica com la del clorur de sodi M=1.75, és a dir, l’energia d’un ió sodi en una xarxa cúbica és un 75% més baixa que en la corresponent molècula diatòmica. Aquesta disminució addicional és deguda a que en el cristall l’ió sodi es troba enllaçat amb tots els ions clorur del cristall. La separació dels ions en el cristall de clorur de sodi és de 2,80� , una mica més gran que en la molècula diatòmica. Aleshores U=-207kcal/mol.

Fins ara hem tingut en compte només l’energia deguda a forces coulòmbiques entre ions considerats com a càrregues puntuals. Degut a la grandària finita del núvol electrònic al voltant de cada ió, existeixen forces repulsives entre ions veïns que no hem inclòs en el càlcul. L’efecte d’aquestes repulsions és fer que l’energia real de la xarxa cristal·lina prop d’un 10% menys negativa que el valor donat per les forces coulòmbiques soles. D’aquesta manera, la veritable energia de la xarxa cristal·lina del clorur de sodi és de -183 kcal/mol. La comparació d’aquest número amb l’energia de la molècula diatòmica –139,5kcal/mol, deixa clar que el cristall és molt més estable i per aquest motiu a temperatura ambient la pressió de vapor és molt baixa.

L’energia que s’allibera quan es forma la xarxa cristal·lina del clorur de sodi és finalment de 35-183 = -148 kcal/mol. Per tant podem dir que el clorur de sodi cristal·lí és més estable que els àtoms gasosos i que l’origen d’aquesta estabilitat és l’atracció coulòmbica dels ions de la xarxa cristal·lina.

Anem a veure ara com calcular l’energia iònica de la xarxa cristal·lina quan es pren en consideració la repulsió entre els ions veïns. La repulsió és deguda a la grandària finita dels ions i és de la mateixa naturalesa que les repulsions de Van der Waals entre àtoms neutres. L’expressió refinada de l’energia potencial és:

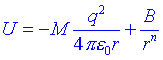
El terme B/rⁿ representa a les repulsions dels àtoms veïns i el valor de n oscil·la entre 9 i 12, segons el tipus de cristall. Generalment es pot avaluar n a partir de la compressibilitat del cristall. El coeficient B mesura la potència de les forces repulsives i és diferent per ions diferents. B es pot eliminar de l’expressió si coneixem el valor de r per al que el cristall és estable, doncs aleshores U és un mínim:

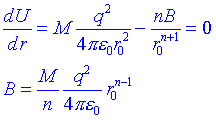
Substituint B a l’expressió de l’energia:

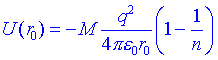
Com que n és aproximadament 10, veiem que l’energia de la xarxa cristal·lina és a prop d’un 10% inferior a l’energia deguda únicament a la interacció coulòmbica. En general hi ha una concordança molt satisfactòria entre els valors calculats i mesurats de la xarxa cristal·lina dels halogenurs dels metalls alcalins.

L’energia de la xarxa cristal·lina augmenta amb el producte de les càrregues dels dos àtoms. Això suggereix que, en els compostos iònics cada àtom ha de tractar d’assolir una càrrega tant gran com sigui possible. Aquesta tendència està limitada pels valors creixents de les successives energies d’ionització dels àtoms. Així doncs, la màxima càrrega positiva està limitada pel nombre d’electrons de valència i la càrrega màxima negativa està limitada pel nombre de vacants que hi ha en els orbitals de valència de més baixa energia. Normalment l’energia de la xarxa no sòl compensar la formació d’ions amb càrregues majors de ± 3.

Es poden utilitzar els radis iònics per comprendre, per exemple, les variacions en les energies de la xarxa cristal·lina dels halogenurs alcalins. Per qualsevol ió positiu donat, l’energia de la xarxa cristal·lina es fa més petita a mesura que l’ió negatiu es fa més gran. La mateixa tendència es troba si s’examinen els compostos d’un ió negatiu qualsevol: l’energia de la xarxa cristal·lina disminueix a mesura que augmenta la grandària de l’ió positiu. Això és lògic si pensem que l’energia de la xarxa cristal·lina depèn de 1/(r₊+r_-).

Podríem suposar que l’augment del nombre de coordinació hauria d’augmentar l’estabilitat de la xarxa. En el clorur de cesi, el nombre de coordinació és 8, la constant de Madelung és de 1,763, mentre que pel clorur de sodi, amb nombre de coordinació 6 és 1,748. D’aquesta manera, amb les mateixes distàncies internuclears, la xarxa cristal·lina del clorur de cesi és un 1% més estable que la del clorur de sodi.

La majoria dels halogenurs però, cristal·litzen en l’estructura de coordinació 6 del clorur de sodi. Això és degut a que quan s’intenta empaquetar 8 ions grans negatius al voltant d’un petit ió positiu central, es troba que la distància de major apropament entre els ions positius i negatius no és determinada per r₊+r_-, sinó pel radi de l’ió negatiu sol. Degut a la grandària, 8 ions negatius es tocaran l’un amb l’altra sense que cap d’ells quedi molt a prop de l’ió positiu. En aquesta situació l’energia de la xarxa cristal·lina no és tant gran com seria possible, ja que la distància entre els ions positius i negatius no és tant petita com r₊+r_- i a més les forces de repulsió entre els ions negatius tan propers seran grans. Si es posen menys ions negatius al voltant de l’ió positiu aleshores l’apropament amb els ions negatius és més gran. A més, la distància entre els ions negatius és més gran, disminuint així les repulsions. D’aquesta manera, quan la diferència de grandàries entre els ions és prou gran, el nombre de coordinació acostuma a ser 6. Quan els ions són de grandàries semblants, com per exemple el CsCl, CsBr i CsI, els ions poden gaudir de l’estabilitat lleugerament major de la coordinació 8.

Anem a veure com es calculen les energies associades als enllaços.

La variació d'energia en una reacció química és deguda fonamentalment a la ruptura i formació de nous enllaços químics. L'energia d'aquests enllaços es determina generalment a partir del següent cicle:

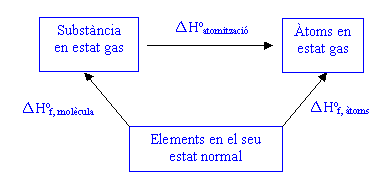
Aleshores:

L'energia de trencament dels enllaços es determina amb els reactius i productes en estat gas, per què d'aquesta manera els canvis energètics són deguts únicament al trencament d'enllaços, no hi ha cap contribució a l'energia necessària per separar les molècules.

El valor exacte de l'energia d'enllaç entre dos àtoms en particular depèn de la molècula en la que es troben, però aquesta dependència és relativament petita, cosa que suggereix que els factors principals que determinen l’energia d’un enllaç particular són les propietats intrínseques dels dos àtoms enllaçats i només en menor grau, les propietats de l’ambient proporcionat per la resta d’àtoms de la molècula.

És útil doncs, calcular un valor promig de l'energia de cada enllaç i tabular-lo. En concret es tabula l'energia mitjana necessària per trencar un mol d'enllaços. D'aquesta manera és possible fer una bona estimació de l'entalpia d'una reacció a partir de les energies d'enllaç:

Anàlogament, també resulta útil conèixer l'energia necessària per formar un cristall iònic a partir dels ions en estat gas. Aquesta magnitud s'anomena energia reticular. L'energia reticular no es pot avaluar directament, si no a través del cicle de Born-Haber.

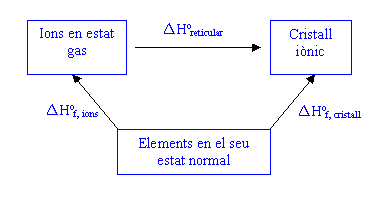
Per tant aleshores:

Si volem calcular l'energia reticular, fixem-nos en què:

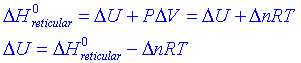
on D n seran els mols de gas desapareguts, i per tant serà un nombre negatiu. El que interessa tabular però és D Hº_reticular a partir de les quals calcularem els calors de reacció quan intervenen substàncies iòniques.

1. Les substàncies iòniques són sòlids cristal·lins.
2. Són poc volàtils i presenten elevats punts de fusió i d’ebullició; aquestes temperatures depenen de les càrregues dels ions. El NaCl (càrregues ± 1) té una temperatura de fusió de 801ºC mentre que el MgO (càrregues ± 2) fon a 2852ºC.
3. Només presenten conductivitat elèctrica si estan fosos.
4. Moltes substàncies iòniques són solubles en aigua o en líquids polars.
5. Són durs i fràgils.

En molts casos es pot saber si un compost és iònic si coneixem la seva composició. En general els cations són ions metàl·lics i els anions són ions no metàl·lics. Per tant, els compostos iònics generalment són combinacions de metalls i no metalls.

Es distingeix entre les substàncies moleculars, formades per molècules discretes que interactuen mitjançant forces de Van der Waals, i sòlids de xarxa covalent.

Els sòlids moleculars consisteixen en molècules (típicament formades per no metalls units amb enllaços covalents) unides per forces intermoleculars: forces dipol-dipol, forces de dispersió de London i ponts d'hidrogen. Com que aquestes forces són dèbils, els sòlids moleculars són tous i tenen punts de fusió relativament baixos (generalment menys de 200ºC). Quasi totes les substàncies que són gasos o líquids a temperatura ambient formen sòlids moleculars a temperatures baixes, com per exemple Ar, CH₄, H₂O i CO₂.

Els sòlids moleculars acostumen a tenir una conductivitat tèrmica molt baixa i en estat pur no són conductors de l'electricitat. Els sòlids moleculars poden ser amorfs (com el vidre), cristal·lins (com el gel) o part amorf part cristal·lí (HDPE).

L'energia d'enllaç dels cristalls moleculars és molt petita comparada amb cristalls iònics o cristalls amb enllaç covalent. Aquests tipus de cristalls tendeixen a ser volàtils i posseeixen punts de fusió i d'ebullició baixos. Els cristalls moleculars tendeixen a ser tous, compressibles i fàcilment deformables. Són, en general, bons aïllants de l'electricitat. Les molècules no tenen càrrega elèctrica neta i per tant no poden transportar electricitat. A més, com que el cristall es composa de molècules discretes, els electrons tendeixen a estar localitzats al voltant d'un grup específic de nuclis. Exemples: H₂O, CO₂, I₂, naftalina, etc.

Els sòlids de xarxa covalent consisteixen en àtoms units en grans xarxes o cadenes mitjançant enllaços covalents. Com que els enllaços covalents són molt més forts que les forces intermoleculars, aquests sòlids generalment són molt més durs i tenen punts de fusió més elevats que els sòlids moleculars. Exemples típics en són el diamant, el carbur de silici SiC i el nitrur de bor BN. Els cristalls covalents són mals conductors de l’electricitat degut a que els electrons en el sòlid estan localitzats en els enllaços covalents i no tenen llibertat de moure’s dins del cristall.

En el diamant cada àtom de carboni està unit a quatre àtoms de carboni formant una matriu tridimensional interconnectada d'enllaços senzills carboni-carboni. El punt de fusió del diamant és de 3550ºC.

En el grafit els àtoms de carboni estan disposats en capes d’anells hexagonals interconnectats. Cada àtom de carboni està unit a d’altres tres de la capa; la longitud de l’enllaç és de 1.42� . Els orbitals p formen enllaços moleculars p deslocalitzats i això fa que el grafit sigui conductor de l’electricitat. Les capes estan separades una distància de 3.41� i es mantenen unides per forces de dispersió. Les capes llisquen fàcilment les unes sobre les altres, cosa que fa apte al grafit per a ser utilitzat com a lubricant i per les mines dels llapis.