TEMA 4
Cinemàtica.
Elements per a la descripció del moviment.
Moviments d'especial interès.
Mètodes per a l'estudi experimental del moviment.
4.1. Cinemàtica
4.2 Elements per a la descripció del moviment
4.2.1 Sistema de referència.
4.2.2 Moviment de la partícula
4.2.3 Velocitat
4.2.4 Acceleració
4.3 Moviments d'especial interès
4.3.1 Moviment uniformement accelerat
4.3.2 Tir parabòlic
4.4 Moviment de rotació al voltant d'un eix fix
4.4.1 Càlcul de la velocitat i l'acceleració
4.4.2 Equacions del moviment en termes de w i a
4.5 Canvis de sistema de referència. Cinemàtica en sistemes de referència no inercials
4.5.1 Canvis de sistema de referència
4.5.2 Sistema de referència no inercial. Sistemes en rotació
4.5.3 Moviment a la superfície de la terra
4.5.4 Sistemes coordenats amb moviment general
4.6 Mètodes per a l'estudi experimental del moviment
4.6.1 L'Estroboscopi
4.6.2 Estudi de moviments molt lents o aparentment lents
4.6.3 Moviment de partícules subatòmiques. Cambra de bombolles.
4.6.4 Mesura de velocitats i acceleracions
4
Cinemàtica. Elements per a la descripció del moviment. Moviments d'especial interès. Mètodes per a l'estudi experimental del moviment.
4.1.
Cinemàtica
La Cinemàtica és la part de la mecànica que descriu la geometria del moviment, sense tenir en compte les causes que el provoquen.
Per al desenvolupament de la mecànica clàssica es pressuposa que l'espai és euclidià i tridimensional i que el temps és absolut, és a dir, és el mateix per a tots els punts de l'espai.
Tractarem el moviment dels cossos com si fossin punts materials. Des d'un punt de vista pràctic això voldrà dir que assumim que les dimensions de l'objecte són menyspreables front a les característiques de la trajectòria. Per exemple quan es descriu el moviment de la Terra al voltant del Sol es pot prendre la Terra com una partícula. A més hi ha un teorema de la mecànica que assegura que el centre de masses de qualsevol objecte es mou com si en ell estés concentrada tota la massa de l'objecte, per la qual cosa la validesa d'aquest tractament és molt general. Estudiarem també el moviment de rotació d'un sòlid. Per acabar, descriurem el moviment d'un sòlid en general, que es pot entendre com una combinació d'una rotació i una translació.
4.2
Elements per a la descripció del moviment4.2.1
Sistema de referència.Estudiar el moviment d'un cos vol dir determinar la posició d'aquest cos en funció del temps. Per a poder fer això necessitem un sistema de referència. A l'espai euclidià un sistema de referència queda determinat amb un determinat punt O, anomenat origen i una base de 3 vectors unitaris i ortogonals que defineixen les tres direccions a l'espai d'un sistema d'eixos cartesians anomenats X,Y i Z. Per a cada eix tindrem un vector unitari paral·lel a l'eix: eix X: i, eix Y: j, eix Z: k. Aquests tres vectors constitueixen una base de l'espai vectorial que es defineix amb l'ajut dels eixos escollits.
La posició de qualsevol mòbil es donarà indicant a quin punt P de l'espai es troba. Qualsevol punt P de l'espai s'identificarà amb un vector amb origen a 0 i final a P. Aquest vector s'anomenarà vector posició r. El vector de posició r s'escriu en funció de les seves projeccions sobre els eixos cartesians (x,y,z) i dels vectors unitaris i ,j ,k. D'aquesta manera:
![]()
4.2.2
Moviment de la partículaLa posició d'un objecte depèn en general del temps, és a dir:
![]()
D'això en diem equació vectorial del moviment. L'extrem del vector r(t) descriu una corba C a l'espai que rep el nom de trajectòria. La trajectòria és el lloc geomètric de les successives posicions que va ocupant l'objecte en el seu moviment.
L'equació vectorial del moviment es pot escriure també especificant per separat el valor de cada coordenada en funció del temps:
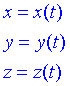
Aquestes equacions determinen una corba a l'espai (la trajectòria) i s'anomenen equacions paramètriques de la trajectòria. En el cas que la trajectòria sigui plana, és a dir, estigui continguda per exemple en el pla xy (z=0), es pot eliminar el temps t i podrem trobar l'equació de la trajectòria plana en forma implícita f(x,y)=0 o explícita y=f(x).
4.2.3
VelocitatConsiderem una partícula que descriu una trajectòria curvilínia. En el temps t està al punt P assenyalat per r(t), i al temps t+D t es situa sobre el punt Q assenyalat per r(t+D t). En passar de P a Q la partícula haurà recorregut un arc de longitud D s. El desplaçament de la partícula ve donat pel vector PQ = D r, de manera que r(t+D t)= r(t)+D r. Es defineix aleshores com a velocitat mitjana el cocient entre D r i D t:
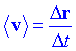
Fixem-nos que <v> té la mateixa direcció que D r i que per tant és secant a la trajectòria. El valor de <v> dependrà del valor de D t. Per evitar aquest inconvenient, és defineix la velocitat en un instant de temps donat t en un punt P com el límit de la velocitat mitjana per D t® 0, és a dir, la derivada del vector de posició respecte del temps:

En el pas al límit, el vector v esdevé un vector tangent a la trajectòria.
Per fer-ho evident en l'expressió de la velocitat, podem calcular el límit de la següent manera: 
![]()
En coordenades cartesianes, i tenint en compte que els vectors i, j, k són constants podem escriure:
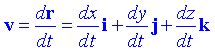
és a dir, que els components del vector velocitat es poden escriure com:
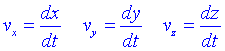
i el mòdul de la velocitat és
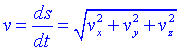
4.2.4
AcceleracióEl vector velocitat, al llarg de la trajectòria, anirà canviant de mòdul i de direcció. Igual que abans podem calcular la variació de velocitat entre dos punts P i Q i definir una acceleració mitjana com el cocient:
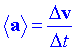
<a> és un vector paral·lel a D v. L'acceleració en un determinat instant de temps es defineix pel pas al límit quan D t® 0:
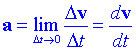
L'acceleració a és un vector en la direcció en la que canvia la velocitat.
Si agafem els vectors velocitat al llarg de la trajectòria i els dibuixem amb un origen comú, els extrems dels vectors velocitats defineixen una corba anomenada hodògrafa. L'acceleració ha de ser tangent a la hodògrafa. Veiem aleshores que si la partícula descriu un moviment circular a velocitat constant, la hodògrafa és també circular i per tant l'acceleració és perpendicular a la velocitat i sobre la trajectòria real assenyala el centre de la circumferència. Si la trajectòria és rectilínia aleshores la hodògrafa també ho serà i el vector acceleració serà paral·lel a la velocitat.
Anem a calcular les components del vector acceleració. En coordenades cartesianes podem calcular directament la derivada:

i les components es poden escriure:

i el mòdul de l'acceleració:
![]()
Anem a escriure ara les components intrínseques del vector velocitat. Sabem que el vector velocitat és tangent a la trajectòria i que el podem escriure com:
![]()
Per trobar l'acceleració derivem respecte del temps:
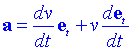
Si la trajectòria fos rectilínia el segon terme seria zero. Anem a calcular la derivada de et respecte del temps. Primer de tot és fàcil demostrar que la derivada ha d'ésser perpendicular a et:
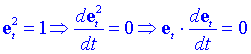
La direcció de la derivada ha d'estar en la direcció en la que varia el vector velocitat, per tant assenyala cap a la banda còncava de la trajectòria.
Considerem dos punts P i P' sobre la trajectòria separats per un ds. Sobre aquests punts podem dibuixar les normals. Les normals es tallaran en un punt C anomenat centre de curvatura i formen entre si un angle dq . La longitud PC = r rep el nom de radi de curvatura. Aleshores és fàcil de veure que: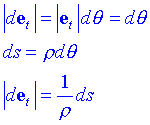
Dividint per dt:

Si anomenem en al vector unitari en direcció a la normal i sentit cap al centre de curvatura, podem escriure:
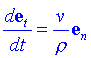
i substituint a l'expressió de l'acceleració arribarem a:
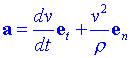
Veiem, doncs que el vector acceleració es pot descomposar en dos components
, una acceleració tangencial a la trajectòria at deguda a la variació del mòdul de la velocitat amb el temps i una acceleració normal a la trajectòria an deguda a la variació de la direcció de la velocitat. Els mòduls d'aquestes components venen donades per:
El mòdul de l'acceleració es pot escriure com:
![]()
4.3
Moviments d'especial interès4.3.1
Moviment uniformement acceleratUn moviment rep el nom d'uniformement accelerat quan a = cte. Integrant l'equació diferencial següent trobarem la dependència de la velocitat amb el temps:
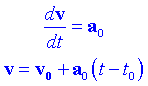
on v0 és la velocitat inicial per t=t0. Per determinar r(t) utilitzem el resultat anterior i integrem un altre cop:

on r0 és la posició inicial per t=t0. Observant les equacions veiem que:
4.3.2
Tir parabòlicAnem a aplicar les equacions anteriors a un moviment amb acceleració constant, el llançament d'un objecte a la superfície terrestre. Com a hipòtesis, suposarem que és menyspreable la curvatura de la superfície de la terra, que el projectil no s'eleva prou com per notar una disminució de l'acceleració de la gravetat i que la resistència de l'aire és menyspreable.
Situem el nostre sistema de referència en el punt de llançament i l'eix X paral·lel a la superfície terrestre. Aleshores:
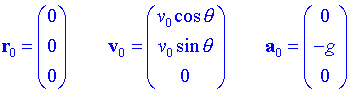
Substituint a les equacions anteriors:

Si eliminem el temps t de l'equació del moviment arribarem a:
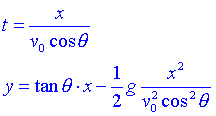
l'equació de la trajectòria.
D'aquestes equacions es pot extreure totes les característiques d'aquest tipus de moviment.
Alçada màxima
L'alçada màxima es produeix quant vy=0. Per tant tindrem:

És obvi que l'alçada més gran es produirà per q =90º.
Abast, temps de vol
Anomenem temps de vol al temps que triga el projectil en arribar al terra, i abast la longitud total recorreguda. El projectil arriba al terra quan y=0. Per tant:
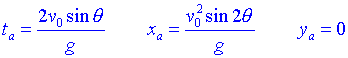
Observem que ta = 2th i que xa = 2xh. El màxim abast es produeix per q =45º i fixem-nos que per q =45º± a l'abast és el mateix independentment del signe, és a dir, l'abast per un determinat angle és el mateix que pel seu complementari.
4.4
Moviment de rotació al voltant d'un eix fix4.4.1
Càlcul de la velocitat i l'acceleracióUn sòlid rígid és un sòlid a on totes les partícules que el composen mantenen una posició relativa constant. Es diu que un sòlid rígid té un moviment de rotació al voltant d'un eix quan tots els seus punts descriuen trajectòries circulars centrades sobre l'eix i contingudes en plans normals a l'eix. Agafem un sistema de coordenades de tal manera que l'origen O estigui contingut en l'eix de rotació.
La velocitat v d'un punt P del sòlid serà tangent a la circumferència. Per tant escriurem:
![]()
El mòdul de la velocitat és la rapidesa:
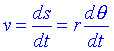
on r és la distància de P a l'eix de rotació i hem utilitzat que ds = rdq amb l'angle en radians. La variació de l'angle respecte del temps rep el nom de velocitat angular w . Podem escriure aleshores:
![]()
La introducció de concepte de velocitat angular és fonamental, degut a que tots els punts del sòlid rígid comparteixen la mateixa velocitat angular. Així doncs la velocitat angular caracteritza el moviment de rotació.
Definirem ara el vector velocitat angular. El vector velocitat angular w tindrà com a mòdul w i com a direcció la de l'eix de rotació. El sentit vindrà donat per la regla de la mà dreta. Escriurem:![]()
on e és un vector unitari en la direcció de l'eix.
Resulta senzill relacionar r (el vector posició de P), la velocitat v i w , doncs fixem-nos que v és perpendicular a w i a r :
![]()
Si derivem respecte del temps trobarem l'acceleració:
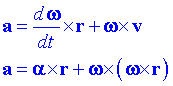
L'acceleració descomposa com la suma de dos termes, un tangent a la trajectòria at i l'altre normal a la trajectòria, anomenada acceleració centrípeta an
:
4.4.2
Equacions del moviment en termes de w i aSi coneixem la velocitat angular o l'acceleració en funció del temps o de l'angle q és possible trobar les equacions del moviment. Pel cas particular en què a =a 0=cte, podem integrar i trobar fàcilment les equacions del moviment:

4.5
Canvis de sistema de referència. Cinemàtica en sistemes de referència no inercials4.5.1
Canvis de sistema de referènciaSuposem que en un sistema fix F s'observa un mòbil el moviment del qual ve descrit pel vector de posició rF. Un altre sistema de referència, l'origen del qual es troba a l'extrem del vector Ro observa també el mòbil amb les seves pròpies coordenades i la posició vindrà donada pel vector rM. La relació entre els tres vectors vindrà donada per:
![]()
Derivant respecte del temps trobarem la relació entre les velocitats i les acceleracions mesurades en tots dos sistemes:
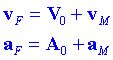
4.5.2
Sistema de referència no inercial. Sistemes en rotacióSi agafem un sistema de referència F amb l'origen sobre un punt de l'eix de rotació i un altre sistema de referència mòbil M, amb el mateix origen, però que gira solidari amb el sòlid rígid. Suposem que l'eix de rotació passa per l'origen. Aleshores:
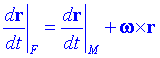
Siguin DF i DM els operadors derivades respecte del temps respecte del sistema F i el M.
Podem escriure aleshores:![]()
Per determinar l'acceleració haurem d'aplicar l'operador DF dues vegades:
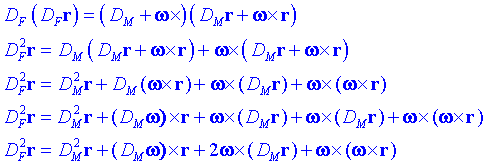
Finalment podrem escriure:
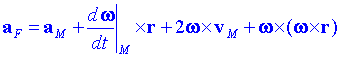
El segon terme rep el nom d'acceleració angular. Els dos últims termes reben el nom d'acceleració de Coriolis i d'acceleració centrípeta.
4.5.3
Moviment a la superfície de la terraA la superfície de la Terra l'acceleració angular és zero, aF = g i per tant es pot escriure:
![]()
L'acceleració de coriolis és perpendicular a la velocitat vista des de la superfície de la Terra i a l'eix de rotació. Aquesta acceleració tendirà, doncs a produir moviments de rotació sobre tot el que es mogui sobre la superfície de la Terra, en particular sobre els corrents d'aire, que en l'hemisferi nord giraran en sentit horari i en l'hemisferi sud antihorari. Fixem-nos, doncs que aquest terme és el responsable de moltes característiques dels sistemes climàtics sobre la Terra. Si la Terra girés a més velocitat (com en èpoques remotes) o menor velocitat els climes locals en les diferents regions del planeta serien força diferents. Els avions comercials també han de realitzar correccions a les seves rutes degut a l'acceleració de coriolis.
L'acceleració centrífuga serà menyspreable en la majoria de casos degut a que depèn de w 2, que és un nombre molt petit.
4.5.4
Sistemes coordenats amb moviment generalAbans hem suposat que tots dos sistemes tenien el mateix origen. Si l'origen no és el mateix, suposem aleshores que el vector R té origen en el sistema F i assenyala l'origen del sistema M. Pel que hem vist abans sobre el canvi de sistemes de referència podrem escriure directament:
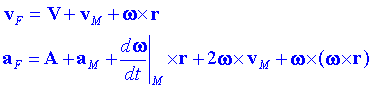
4.6 Mètodes per a l'estudi experimental del moviment
4.6.1
L'EstroboscopiL'estroboscopi, conjuntament amb la càmera fotogràfica (o de cinema) és una eina fonamental per a l'estudi del moviment d'objectes que es mouen a gran velocitat o que realitzen moviments periòdics.
L'estroboscopi és un aparell que produeix un cert nombre de ràfegues de llum o flaixos per unitat de temps. La durada d'aquest flaixos és important i depèn de quin sistema es faci servir per produir-los. Actualment és possible produir feixos molt intensos de llum d'una durada inferior a 3m s i repetir-los més de 5.000 vegades per segon (T=200m s).
a. Estudi de moviments molt ràpids
Quan s'ha d'estudiar el moviment de fenòmens que succeeixen en intervals de temps molt curts, com el moviment de projectils o el moviment de les ales d'un colibrí es fa necessari l'ús de tècniques estroboscòpiques per a l'enregistrament fotogràfic d'imatges. El Dr Harold Edgerton en fou el pioner.
Quan es vol prendre una sola imatge d'un esdeveniment (exemple, l'impacte d'una bala contra una poma) cal que la durada del flaix sigui extremadament curta, perquè si no la imatge ens sortirà moguda. Mitjançant el desenvolupament del flaix electrònic és possible produir un únic feix de llum d'una durada propera a la milionèsima de segon. D'aquesta manera és possible "congelar" el moviment d'objectes molt ràpids en una única imatge fotogràfica.
Per observar l'evolució d'un moviment ràpid hi ha dues possibilitats:
i) La primera consisteix en fer una única fotografia, amb l'objectiu obert i amb un estroboscopi en funcionament. D'aquesta manera s'obté una superposició de les diferents posicions de l'objecte en funció del temps. Com que l'interval entre flaixos és conegut, mitjançant l'estudi de la fotografia obtinguda és possible determinar la velocitat de l'objecte (a partir de la distància sobre la fotografia de dues posicions consecutives de l'objecte) o fins i tot l'acceleració (a partir de la variació de la distància).
ii) La segona consisteix en fer-ne una pel·lícula a alta velocitat. La càmera que enregistra la pel·lícula està sincronitzada amb un estroboscopi. D'aquesta manera es poden obtenir fins a 5.000 fotogrames per segon (T=200m s).
b. Estudi de moviments periòdics
L'estroboscopi és una eina que s'utilitza a la indústria per a la inspecció de màquines que realitzen moviments periòdics, o com a cas particular moviments de rotació. De fet el problema de poder inspeccionar motors i mecanismes girant a velocitats elevades va ser el que va portar al Dr Edgerton al desenvolupament de l'estroboscopi.
L'estroboscopi permet veure un objecte en rotació com si estés parat. Això s'aconsegueix igualant el nombre de flaixos per minut al nombre de revolucions per minut que doni l'objecte. D'aquesta manera es pot calcular amb gran precisió la velocitat de gir i es pot inspeccionar el funcionament de l'objecte. Un estroboscopi comercial pot arribar a produir flaixos de 10 m s unes 30.000 vegades per minut (T=2ms).
4.6.2
Estudi de moviments molt lents o aparentment lentsL'estudi de moviments molt lents es du a terme mitjançant tècniques fotogràfiques o amb càmeres CCD. Fotografiant o enregistrament amb vídeo amb l'ordinador la imatge de l'objecte cada cert nombre d'hores o dies s'obtenen imatges successives que en permeten deduir les característiques del moviment. Aquesta tècnica s'utilitza per exemple per determinar la trajectòria d'objectes celestes (cometes, asteroides, estels, etc…) o per visualitzar el moviment de les flors quan s'obren…
4.6.3
Moviment de partícules subatòmiques. Cambra de bombolles.Una cambra de bombolles és un dispositiu que permet visualitzar les trajectòries de partícules elementals que normalment han estat accelerades fins a velocitats properes a la de la llum.
Hi ha molts dissenys, però el més senzill consisteix a sotmetre hidrogen líquid a una pressió elevada i a una temperatura lleugerament per sota de la temperatura d'ebullició. La temperatura d'ebullició depèn de la pressió. Si es baixa la pressió bruscament, també baixa bruscament la temperatura d'ebullició, de manera que l'hidrogen líquid manté una temperatura que esdevé superior a la d'ebullició. En aquest estat, la més mínima pertorbació produeix la formació de bombolles.
Quan una partícula elemental amb càrrega elèctrica entra a la cambra, ionitza àtoms d'hidrogen al llarg de la seva trajectòria. Els electrons alliberats perden ràpidament la seva energia xoquen amb altres àtoms. Això produeix un escalfament petit però suficient com per produir bombolles. D'aquesta manera apareixen bombolles als punts de la trajectòria que ha seguit la partícula. Les partícules neutres no poden ionitzar àtoms d'hidrogen i per tant no deixen cap rastre.
Les bombolles es poden fotografiar fàcilment de manera que a posteriori els científics puguin extreure'n informació. Per això, Dues de les parets de la cambra són de vidre. Per una banda, s'il·lumina amb un flaix potent i per l'altre es forma la imatge amb l'ajut d'una o més càmeres.
Normalment es sotmet la cambra de bombolles a un camp magnètic molt potent. D'aquesta manera les partícules segueixen trajectòries circulars o en espiral. Partícules de càrrega diferent giren en direccions diferents, i la curvatura depèn de l'energia i de la massa de la partícula. D'aquesta manera s'han pogut identificar i determinar la massa i el temps de vida de centenars de partícules subatòmiques.
4.6.4
Mesura de velocitats i acceleracions


