TEMA 29
Limitacions de la física clàssica
Mecànica relativista.
Postulats de la relativitat especial.
Algunes implicacions de la física relativista.
29.1
Limitacions de la física clàssica
29.2 Postulats
29.3 Les transformacions de Lorentz
29.4 Conseqüències immediates
29.4.1
La Simultaneïtat depèn del sistema de referència29.4.2 Dilatació del temps
29.4.3 Contracció de longituds
29.4.4 Un exemple de la dilatació del temps i la contracció de longituds.
29.5 Suma de velocitats
29.6 Espai-Temps
29.6.1
Les transformacions de Lorentz lliguen espai i temps29.6.2 4-vectors. Producte escalar
29.7 Cinemàtica
29.7.1
Parametrització de les equacions del moviment29.7.2 4-vector velocitat i acceleració
29.7.3 Acceleració uniforme longitudinal
29.8 Mecànica Relativista
29.8.1
Conservació del moment
29.9 Exemples daplicació de la mecànica relativista: conservació del moment
29.9.1
Decaïment dun àtom excitat29.9.2 Aniquilació Positró-Electró
29.9.3 Dispersió Compton
29.10. Efecte Doppler
29
Limitacions de la física clàssica. Mecànica relativista. Postulats de la relativitat especial. Algunes implicacions de la física relativista
.29.1
Limitacions de la física clàssicaEl principi de relativitat va ser establert per primer cop com a corolari de les seves lleis del moviment de Newton. El principi de relativitat estableix que les lleis de la mecànica són les mateixes per tots els sistemes de referència inercials.
En la mecànica Newtoniana el canvi de sistema de coordenades entre dos sistemes de referència inercials sescrivia com (suposant els eixos paral·lels i la velocitat relativa de desplaçament sobre leix de les x):
![]()
Aquesta transformació rep el nom de transformació de Galileu. Si sobre les lleis de Newton efectuem aquestes transformacions les lleis de Newton resulten ser invariants.
Posteriorment, estudis molt rigorosos sobre electricitat, magnetisme i òptica porten a la formulació de les equacions de Maxwell del camp electromagnètic, que permet descriure lelectricitat, el magnetisme i lòptica amb una única teoria. Les equacions de Maxwell no van mostrar mai en aquella època cap discrepància amb els experiments. Però les equacions de Maxwell no són invariants sota la transformació que hem escrit abans.
Si el principi de relativitat era cert per les equacions de Maxwell, això volia dir que la llum sempre viatjava a la mateixa velocitat independentment del sistema de referència i de la velocitat de lemissor. I aquest fet va ser comprovat experimentalment per Michelson i Morley en el seu famós experiment. Per tant, això volia dir, que la llei de transformació que hem escrit abans no era correcta. També indicava, en contra del que es creia en aquella època, que no hi havia cap èter sobre el que es propagava la llum, lexistència del qual hagués permès mesurar la velocitat absoluta de qualsevol sistema de referència respecte de lèter.
Primer Lorentz, amb una validesa més restringida, i després Poincaré amb una formulació de validesa general, van demostrar que les equacions de Maxwell eren invariants sota la transformació següent:
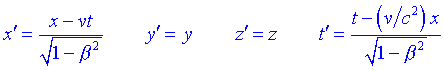
on b = v/c i k (v) una constant depenent de la velocitat. Poincaré suggerí aleshores que potser totes les lleis de la física havien de ser de tal manera que havien de romandre invariants sota les transformacions de Lorentz.
Einstein segueix el suggeriment de Poincaré i se nadona, que les equacions de Lorentz es poden deduir a partir de dos postulats senzills, a partir dels quals caldrà construir una nova mecànica: la mecànica relativista.
29.2
PostulatsEinstein va demostrar que era possible obtenir les transformacions de Lorentz a partir daquests postulats:
Aquests dos postulats constitueixen el punt de partida del desenvolupament de tota la teoria de la relativitat especial. La teoria electromagnètica clàssica que sexpressa mitjançant les quatre equacions de Maxwell verifica de manera natural els dos postulats, i de fet en constitueixen la font dinspiració.
29.3
Les transformacions de LorentzAnem a derivar ara les transformacions de Lorentz fent ús dels dos postulats. Considerem una font de llum puntual que es mou respecte dun sistema de referència S(x,y,z,t) amb velocitat v, i considerem un segon observador S(x,y,z,t) en repòs respecte a L. Ambdós observadors han de veure fronts dona esfèrics amb centres en repòs respecte de S i de S. A partir daquest fet, podem derivar la transformació que connecta les coordenades (x,y,z,t) amb les coordenades (x,y,z,t) de dos sistemes de referència S i S en moviment relatiu uniforme. Leix x lescollim de manera que coincideixi amb la direcció del moviment. Així, S es mou respecte de S amb velocitat v en la direcció x positiva. Les transformacions hauran de verificar:
![]()
aleshores lequació del front dones a S sha de poder escriure com:
![]()
la transformació shaurà de reduir a la galileana.
Podem intentar la següent transformació:
![]()
on g i g hauran de tendir a la unitat i haurà de tendir a zero per ![]() . Substituint en lequació del front dona esfèric obtenim:
. Substituint en lequació del front dona esfèric obtenim:
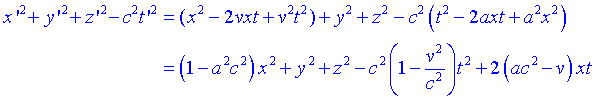
Per començar, el terme lineal ha de ser nul, per tant
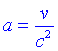
Substituint obtenim:
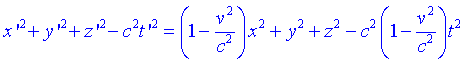
Per tant la transformació no és satisfactòria. Ens apareix un factor descala (1-v2/c2) que resulta fàcil deliminar. Per tant les transformacions es poden escriure definitivament com:
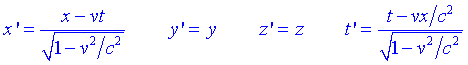
A part de derivar les transformacions de Lorentz, hem arribat a un altre resultat que més endavant veurem que és de fonamental importància. La quantitat ![]() té el mateix valor en tots els sistemes de referència inercials. Diem doncs que és una magnitud escalar.
té el mateix valor en tots els sistemes de referència inercials. Diem doncs que és una magnitud escalar.
29.4
Conseqüències immediates
29.4.1
La Simultaneïtat depèn del sistema de referènciaSuposem dos esdeveniments (t1, x1) i (t2, x2) que a S succeeixen instantàniament, és a dir, t1=t2. Aquests dos esdeveniments poden ser per exemple dues explosions simultànies en dos punts diferents sobre leix X. Anem a utilitzar les transformacions de Lorentz per veure que es veu a S:
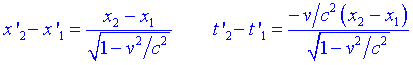
A S, veuen les dues explosions separades per una distància més gran. A més succeeixen en instants diferents de temps i quina de les dues explosions és la primera depèn de la posició de les explosions: la que està més a lesquerra sempre és la que succeeix primer respecte de S.
29.4.2
Dilatació del tempsSuposem que un determinat fenomen, que té lloc a S en un punt x0, comença en el temps t1 i acaba en el temps t2. El fenomen, doncs, dura un temps t = t2-t1. A t se lanomena temps propi. A S, el mateix fenomen dura un temps:
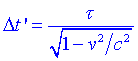
que resulta ser superior. Per tant a S el temps sembla que es dilati. Exemple: una partícula subatòmica inestable dura més temps si es mou a una velocitat propera a la de la llum que si roman estacionària.
Hi ha una manera de deduir aquest resultat directament dels principis bàsics. Suposem que construïm un rellotge ("Rellotge dEinstein") que consisteix en dos miralls paral·lels, situats un damunt de laltra. Quan es produeix un feix de llum vertical, la llum comença a anar cap amunt i cap avall, i suposem que fa clic cada vegada que la llum arriba al mirall de sota. Posem ara un rellotge dEinstein a S i un altre a S prèviament sincronitzats. Anem a veure que passa a S respecte de S. Veiem que a S la llum ara es veu obligada a recórrer un camí en forma de ziga-zaga. Aquest camí és més llarg que el camí que la llum ens fa a S, i com que la velocitat de la llum és la mateixa en tots dos sistemes, deduïm que el temps passa més lentament a S. Anem a veure si deduïm la mateixa expressió.
La meitat de la base de la ziga-zaga és ½V·t . Cada costat mesura ½ c·t . La separació dels miralls és L. Respecte de S, la llum puja i baixa en un temps D t i per tant L= ½c·D t. Per Pitàgores:
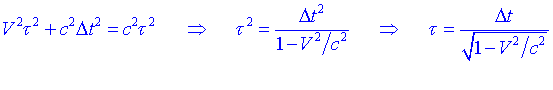
29.4.3
Contracció de longitudsConsiderem una vareta al llarg de leix X en el sistema S. Com que està en repòs les coordenades de posició dels seus extrems són x1 i x2 i aquestes coordenades són independents del temps. La longitud de la barra, que anomenem longitud pròpia sescriu com L0 = x2-x1.
Examinem la vareta des del sistema de referència S. Determinem la longitud de la vareta L=D x en un instant t. Aleshores:
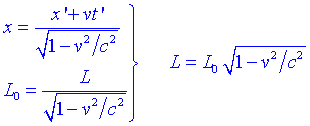
Per tant, un objecte en moviment és més curt en la direcció del moviment respecte dun sistema en repòs.
29.4.4
Un exemple de la congruència entre la dilatació del temps i la contracció de longituds.Suposem a S un feix de llum que surt dun colimador i que va a parar a una cèl·lula fotoelèctrica. Un sistema com aquest es pot utilitzar per mesurar longituds. Suposem que coneixem la velocitat dun mòbil solidari amb S que es mou perpendicularment al feix. Quan travessa el feix, linterromp durant un cert temps D t. Per tant diem que lobjecte deu tenir una longitud L equivalent a:
![]()
Els que viuen dins de lobjecte diuen, però, que són travessats pel feix durant un temps més gran, degut a la dilatació del temps. Per tant:
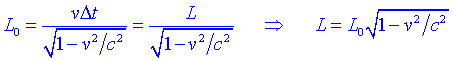
Arribem a la conclusió que la longitud que hem mesurat a S és més curta que la que és mesura en el sistema propi S.
29.5
Suma de velocitatsSuposem que una partícula es mou amb velocitat (vx, vy, vz) respecte al sistema S. Quines són les components de la velocitat (vx, vy, vz) al sistema S? Per respondre aquesta pregunta escrivim les transformacions de Lorentz i diferenciem:
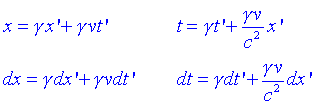
Aplicant la definició de velocitat:
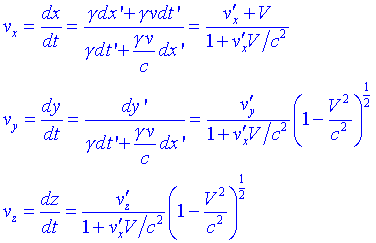
Podem comprovar que la velocitat de la llum no depèn del sistema de referència. Si fem vx = c, obtenim vx = c.
Suposem ara que la velocitat de la partícula a S és perpendicular a V, és a dir, tenim que la velocitat és per exemple: (vx = 0, vy, vz = 0). En aquest cas les equacions són molt més simples:
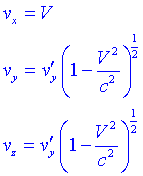
Fixem-nos que el factor que ens apareix és purament degut a la dilatació del temps.
29.6
Espai-Temps
29.6.1
Les transformacions de Lorentz lliguen espai i tempsHem vist com el canvi de coordenades entre dos sistemes de referència inercials ve donat per les transformacions de Lorentz. Aquestes transformacions permet passar de lobservació dun determinat esdeveniment (t,r) a S al corresponent esdeveniment (t,r) a S, on S és un sistema inercial que es mou a velocitat v respecte de S. Agafant els eixos convenientment i escollint c=1 (equivalent a prendre com a unitat de longitud la distància que la llum recorre en un segon) podem escriure les transformacions com:
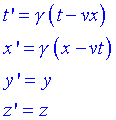
Podem observar la brutal meravellosa i simple simetria entre x i t i la importància didentificar un esdeveniment amb el temps i les tres coordenades espacials. El fet que un canvi de sistema de referència impliqui indissolublement tots 4 nombres en els dos sistemes, suggereix de forma immediata que lespai físic és un espai de 4 dimensions format per tots els esdeveniments (t,r) possibles. És a dir, el temps és una coordenada i les altres tres són les coordenades espacials. A aquest espai de 4 dimensions lanomenem espai-temps.
29.6.2
4-vectors. Producte escalarUn canvi de sistema de referència inercial representa un canvi de coordenades de lespai-temps que sexpressa mitjançant les transformacions de Lorentz. Queda clar doncs que a partir dara treballem en 4-dimensions. De manera anàloga a com vam fer en lespai euclidià de tres dimensions, definim ara un 4-vector com un conjunt de 4 quantitats (at, ax, ay, az) que es transformen com (t,x,y,z) quan canviem a un altre sistema de referència inercial. És a dir, que per saber si un conjunt de 4 quantitats a S constitueix un quadrivector hem de comprovar podem utilitzar les transformacions de Lorentz per calcular les corresponents quatre quantitats a S. Hi ha moltes maneres descriure 4-vectors, nosaltres els escriurem com am = (at, a).
Quan varem deduir les transformacions de Lorentz vàrem veure que tenen una propietat important: donat un determinat esdeveniment amb coordenades (t,r) a S i el corresponent esdeveniment (t,r) a S la següent quantitat roman invariant:
![]()
A partir daquí traurem conseqüències fonamentals. Fixem-nos en lestructura daquesta igualtat. Hi intervenen totes les coordenades elevades al quadrat i el resultat és un escalar. La validesa daquesta invariància és general per tots els quadrivectors: la invariància no depèn de que representen les coordenades, si no que únicament prové del fet que els quadrivectors es transformin segons les transformacions de Lorentz. Per tant per a qualsevol quadrivector tindrem:
![]()
Un pas més. Suposem que tenim dos 4-vectors am i bm . Com que tots dos conjunts de quantitats es transformen de la mateixa manera, la combinació:
![]()
és també una quantitat escalar.
29.7
Cinemàtica
29.7.1
Parametrització de les equacions del movimentA la mecànica Newtoniana, la trajectòria duna partícula ve en general donada per la funció r(t). En aquest tractament, la característica fonamental de t és que linterval dt entre dos instants de levolució de la partícula és invariant, és a dir, té el mateix valor a qualsevol sistema de referència inercial no relativista. Diem que a la mecànica newtoniana el temps és un paràmetre invariant.
Amb la modificació relativista, t ja no és un paràmetre invariant. Seguint Minkowski, convé representar sobre lespai temps levolució de la partícula, que serà una línia continua (anomenada línia de lunivers) La línia de lunivers és una corba 1-dimensional i per tant per definir-la caldrà donar les quatre coordenades en funció dun paràmetre que caldrà que sigui invariant. En particular resulta convenient prendre s on s ve definit com:
![]()
i com ja sabem, és una magnitud invariant. Aquesta expressió es pot rescriure fàcilment en termes del temps propi de la partícula:
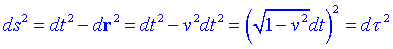
Per tant en el sistema de la partícula ds = dt . Per tant el paràmetre natural per descriure el moviment de la partícula és el seu temps propi.
29.7.2
4-vector velocitat i acceleracióPrenent s ò t com a paràmetre natural sescriu la velocitat duna partícula com:
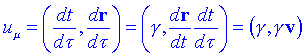
Una propietat important daquesta definició és que:
![]()
Definim anàlogament la 4-acceleració com:
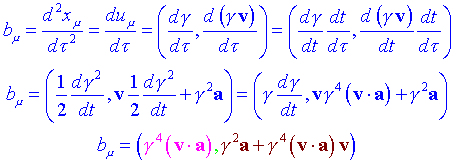
En el sistema solidari amb la partícula, la 4-velocitat i la 4-acceleració es poden escriure com:
![]()
Anem a relacionar ara lacceleració a que es veu en el sistema de la partícula i lacceleració a que es veu en el sistema S. Suposem que la velocitat de la partícula està en la direcció x. Aplicant les transformacions de Lorentz tindrem que:
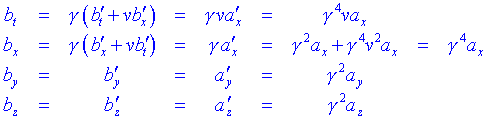
Per tant tenim que:
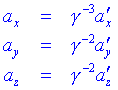
29.7.3
Acceleració uniforme longitudinalAnem a suposar que lacceleració és paral·lela a la velocitat i constant en el sistema de la partícula. Suposem un coet que crema el seu combustible de manera que lacceleració que mesura lacceleròmetre del coet doni un valor constant. Agafem leix X paral·lel a la velocitat podem escriure ax = a i la resta de components zero. Considerarem que per t=0, x=0 i v=0. Lacceleració en el sistema S sescriurà com:
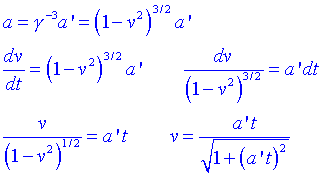
Per tant la velocitat tendeix assimptòticament a la velocitat de la llum. Si tornem a integrar:
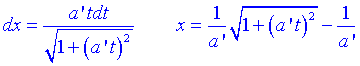
trobem la dependència de x amb el temps.
29.8
Mecànica RelativistaDos principis bàsics de la Mecànica Clàssica són la conservació del moment i la conservació de lenergia. El moment era un vector amb tres components espacials i lenergia una magnitud escalar. En la mecànica relativista, la situació canvia radicalment i sestableix una relació molt més profunda entre moment i energia.
Començarem pensant com definir en lespai-temps un quadrivector moment duna partícula que mou a velocitat v. Aquest quadrivector, el podrem definir com el producte de la massa en repòs de la partícula en consideració (una magnitud escalar per definició) amb el quadrivector velocitat:
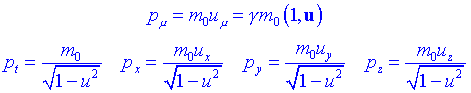
Quin significat té la component pt? Per esbrinar-ho, anem a veure que passa si considerem velocitats petites, és a dir, ![]() Per tant, recuperarem les c i desenvolupem en sèrie de Taylor:
Per tant, recuperarem les c i desenvolupem en sèrie de Taylor:
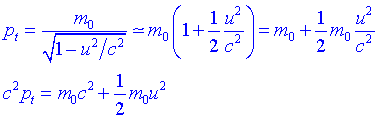
El segon terme és lenergia cinètica Newtoniana. Seguint a Einstein, direm aleshores que la component temporal del 4-vector moment és lenergia total duna dividida per c2, i que el primer terme del desenvolupament representa lenergia en repòs de la partícula.
Si calculem el mòdul del 4-vector moment:
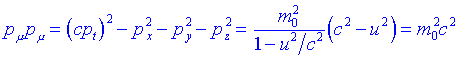
El mòdul és un valor constant que equival a lenergia en repòs al quadrat dividida de c2. Si escrivim pt en termes de lenergia obtenim:
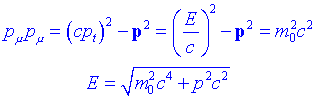
Hi ha una partícula a la Natura que té massa en repòs nul·la, el fotó, i aleshores el mòdul del 4-vector moment té mòdul zero. Per un fotó podem escriure aleshores:
![]()
Resulta interessant aplicar les transformacions de Lorentz a pm per passar dun sistema inercial S a un altre sistema inercial S (c=1):
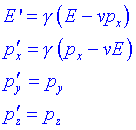
Veiem que el que a S sanomena energia, és una barreja del que anomenem energia i moment en el sistema S. Anàlogament pel que anomenem moment. El moment i lenergia estan tant relacionats entre si com lespai i el temps.
29.8.1
Conservació del momentSuposem que tenim una colecció de partícules que constitueixen un sistema aïllat, cadascuna amb el seu propi 4-vector moment. Postulem aleshores que la suma de moments equival a un 4-vector constant:
![]()
Si Cm és un vector constant a S, també ho serà a qualsevol altre sistema inercial S, degut a lestructura de les transformacions de Lorentz. Fixem-nos, doncs que la validesa daquesta llei implica simultàniament la conservació de lenergia i del moment. De fet, en la mecànica relativista, la conservació de lenergia i la conservació del moment són inseparables i dependents luna de laltra.
La validesa de la llei de conservació del moment només es pot establir experimentalment. En els apartats següents exposarem diverses situacions que han permès comprovar la validesa daquesta llei.
29.9
Exemples daplicació de la mecànica relativista: conservació del momentLa classe dexperiments que volem analitzar tindran la forma:
![]()
La conservació del moment i de lenergia sescriurà com:
![]()
Tindrem com a dades els quadrivectors A i B i haurem de donar alguna informació sobre C o D. Si suposem que només hi ha dues partícules resultants C i D i que ens interessa especialment que li passa a C. Escriurem aleshores:
![]()
i elevant al quadrat:
![]()
daquesta manera només ens queda com a incògnites magnituds relacionades amb C.
29.9.1
Decaïment dun àtom excitat Suposem que un àtom excitat és mou sobre leix x i emet un fotó. El fotó surt formant un angle j amb leix x. Escrivim ![]() Volem calcular la dependència de lenergia del fotó Eg amb langle demissió g . Escrivim:
Volem calcular la dependència de lenergia del fotó Eg amb langle demissió g . Escrivim:
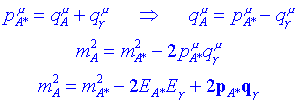
Com que el fotó té massa zero, aleshores qg = Eg . Substituint:
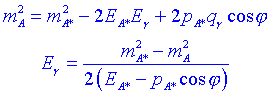
29.9.2
Aniquilació Positró-ElectróQuan un electró i un positró es troben emeten dos raigs g . Suposem el positró parat, lelectró que sapropa per leix x i després de la col·lisió, els dos fotons g formant els angles j 1 i j 2 amb leix x (un per sobre i laltre i per sota). Volem calcular quina és lenergia en funció de langle que fan els dos fotons. La llei de conservació es pot escriure com:

Anem a veure que passa amb el fotó 1. Elevant al quadrat:
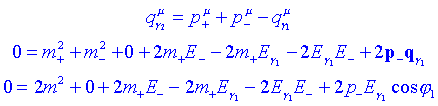
Arreglant lexpressió podem calcular Eg 1:
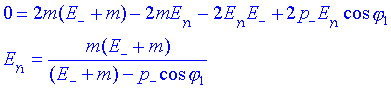
Si el fotó 1 és emès cap a la dreta (j 1=0) aleshores la seva energia és màxima. Per tant aleshores el fotó 2 serà emès amb la mínima energia possible amb j 2 = p .
29.9.3
Dispersió ComptonSuposem ara un electró en repòs que interacciona amb un fotó que és dispersat. El problema que ens plantegem és trobar lenergia del fotó dispersat en funció de langle entre el fotó incident i el fotó dispersat. Seguim, doncs el mateix procés:
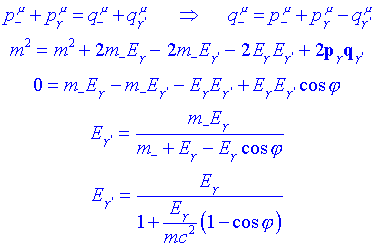
Aquesta expressió normalment es rescriu en termes de les longituds dones. Per a un fotó ![]() Substituint:
Substituint:
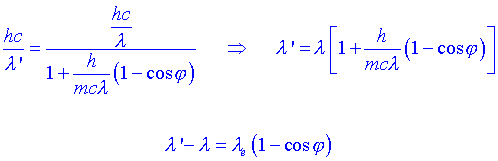
on l e és lanomenada longitud dona de compton 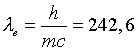 .
.
29.10.
Efecte DopplerAnem a descriure ones que es propaguen en el buit. Comencem considerant una ona plana monocromàtica:
![]()
La fase de lona és una magnitud escalar. Considerant un sistema S i un sistema S com de costum, si la fase de lona és un escalar shaurà de verificar que:
![]()
Si la fase de lona és un escalar, i (t, r) és un 4-vector, podem concloure aleshores que ![]() també és un quadrivector. La fase de lona és el producte escalar de dos 4-vectors. Per tant podem escriure:
també és un quadrivector. La fase de lona és el producte escalar de dos 4-vectors. Per tant podem escriure:
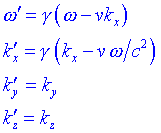
Si escrivim:
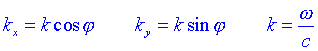
on j és langle que forma k i leix x, obtenim per la freqüència la següent expressió:
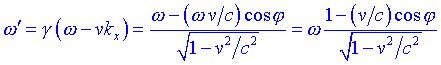
Si ![]() (és a dir, lona es propaga en la direcció x) aleshores:
(és a dir, lona es propaga en la direcció x) aleshores:
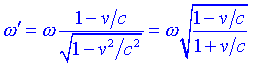
Aquest resultat també es pot escriure en termes de les longituds dona:
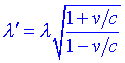
Si una Galàxia sens allunya, observarem un increment de les longituds dona de lespectre, conegut com a corriment cap al vermell. Si la Galàxia sapropa observarem lefecte contrari, i parlem de corriment cap al blau.