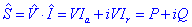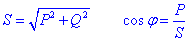---

Elements d’importància
en els circuits electrònics

En el món elèctric hi ha un cert nombre d’objectes que es poden connectar per a fer circuits elèctrics. S’anomenen elements actius d’un circuit les fonts de tensió o d’intensitat que proporcionen energia a un sistema elèctric. Es consideren passius aquells elements que pernen energia de generadors per a transformar-la en algún altre tipus d’energia o acumular-la en forma de camp elèctric o de camp magnètic. Anem a estudiar-ne tres dels anomenats elements passius de circuit: condensador, resistència i bobina o inductància. estudiarem també el comportament elèctric d'aquests elements en circuits de corrent altern.

Constitució i característiques bàsiques de les resistències

Anomenem resistència a un element de circuit en el que la quantitat de corrent que el travessa és proporcional a la diferència de potencial que se li aplica. Diem doncs que verifica la llei d’Ohm i que podem escriure:

Les resistències es poden fer servir en els circuits per a controlar la intensitat de corrent i constitueixen l’element elèctric més simple. Les resistències estan formades per un material de resistència coneguda recobert per una capa aïllant. De la capa aïllant en surten dos terminals per a poder-ne realitzar les connexions. La fabricació de les resistències es basa en el fet que la resistència d’un conductor es pot escriure com:

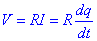
on rho depèn de la naturalesa del conductor, L la longitud i S la secció del conductor.

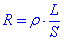
Tipus de resistències

Com que el pas de corrent elèctric per una resistència implica l’alliberament de calor, distingim entre:

• Resistències de baixa potència: 1/8W - 2W
• Resistències de potència: a partir de 2W

Distingim també entre resistències fixes i variables. Comencem per les fixes. Segons la seva fabricació distingim entre:

• Resistències aglomerades : El procés bàsic de fabricació consisteix en formar barres compostes de grafit i una resina aglomerant. Variant la secció, la longitud i la resistivitat de la mescla s’obtenen els valors normalitzats. Posteriorment es monten els terminals de sortida sobre el cos resistiu, es recobreix el conjunt amb una capa aïllant i es marca el codi colors. Aquest tipus de resistències suporten bé les sobrecàrregues d’intensitat.
• Resistors de película de carbó : Estan constituides per un suport ceràmic on s’hi diposita carbó. Després mitjançant làser o diamant es fa un espiralat en funció del valor de la resistència que es vol obtenir. L’espiralat fa que el procés de fabricació sigui equivalent a haver enrotllat una tira de carbó sobre el suport ceràmic. Després es col·loquen els terminals i es cobreix el conjunt amb resines o laques. Tot el conjunt s’introduiex en un forn per a endurir la resistència i finalment es marca el valor nominal. Són les més comunes i es fabriquen amb toleràncies del 5%.
• Resistors de película metàl·lica : Es fabriquen de manera molt similar a les de pel·lícula de carbó, però en lloc de carbó es fa servir metalls: Molibdè, crom, wolframi i titani. Són molt estables i fiables i s’utilitzen en treballs de precisió. Es fabriquen amb toleràncies del 2% i del 1%. Es fabriquen per a potències 0,4-0,75W
• Resistències bobinades : El principi de construcció consisteix en enrotllar sobre un suport ceràmic un fil o cinta amb una determinada resistivitat. Hi ha diverses maneres d’enrotllar el fils: bobinat pla, bobinat de fils paral·lels, bobinat Airton Perry; aquest dos últims es fan per a minimitzar el valor de la inductància. Normalment es fan servir al·leacions de Ni-Cr-Al i en situacions de precisió al·leacions de Ni-Cr (80/20). Existeixen varios models: Cimentades, vitrificades, Pintades, etc. Es fan servir en resistències de potència.

De resistències variables en tenim de dos tipus, els reòstats i els potenciòmetres:

• Els reòstats tenen un punt de connexió fix i un altre de mòbil. Estan formats per un fil bobinat sobre un suport aïllant en forma de corona circular. S’utilitzen per a variar els valors de la resistència en circuits de potència.
• Els potenciòmetres tenen dos punts de connexió fixos i un altre de mòbil que s’anomena cursor. Poden estar formats per pistes de carbó o per bobines. N’hi ha de diferents tipus: de carbó, bobinats, ceràmics, trimmers, etc.

Potència consumida per un resistència

La diferencia de potencial en una resistència ens indica el treball per unitat de càrrega necessari per travessar la resistència. La intensitat ens indica quantes càrregues per unitat de temps travessen la resistència, per tant, l’energia consumida a la resistència es pot escriure fàcilment com P = I·V = R·I². Aquesta potència apareix en forma de calor a la resistència.

Constitució i característiques bàsiques dels condensadors

Els condensadors són elements que emmagatzemen una quantitat de càrrega que és proporcional a la diferència de potencial al que se’l sotmet. Poder dir doncs que són dispositius que acumulen energia elèctrica. Si la tensió varia el condensador pot absorvir o cedir les càrregues i l’energia acumulada. S’anomena capacitat a la constant de proporcionalitat que relaciona la càrrega i el potencial:

L’estructura bàsica d’un condensador correspon a dues plaques o làmines conductores separades per un material dielèctric. La capacitat del condensador és proporcional a la superficíe de les plaques i la permitivitat elèctrica del dielèctric i és inversament proporcional a la distància entre les plaques. Els condensadors es poden carregar fins a un cert límit, perquè si la tensió supera la rigidesa del dielèctric el dielèctric esdevé conductor i es perfora. Així doncs, un condensador s’identifica segons la seva capacitat i la tensió màxima de treball. També cal indicar la tolerància en el valor de la capacitat.

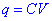
Tipus de condensadors

Hi ha condensadors fixes, variables i ajustables. Comencem pels fixos:

• De paper impregnat : El dielèctric és de cel·lulosa impregnat amb olis o parafines. Es construeixen enrotllant dues làmines metàl·liques separades del dielèctric. Són robusts i suporten sobretensions.
• De paper metal·litzat : es fabriquen amb un dipòsit d’alumini sobre una de les cares del dielèctric (cel·lulosa) i enrotllant. La principal característica d’aquest condensador és l’autoregeneració: si en algún punt del condensador salta una espurna, l’arc elèctric vaporitza l’alumini formant-se alúmina, que és un material dielèctric. Són petits i estables front a canvis de temperatura.
• De plàstic: Els dielèctrics més utilitzats són poliestirè, polipropilè, teflon, etc. El dielèctric és un bon aïllant, la qual cosa permet conservar la càrrega durant molt de temps. Són relativament petits i tenen autoregeneració els de poliéster metal·litzat.
• De mica : Són condensadors estables que poden soportar tensions elevades, doncs la mica presenta una rigidesa elèctrica elevada.
• Ceràmics : La ceràmica és un bon aïllant elèctric. El procés de fabricació consisteix bàsicament en la metal·lització de les dues cares del material ceràmic.
• Electrolítics : Presenten una gran capacitat front a la seva grandària. Això és degut a que el dielèctric té una permitivitat elevada i a més es poden aconseguir capes molt primes. Hi ha dues grans famílies: els d’alumini i els de tàntal. El fonament és el mateix per tots dos: dipositar mitjançant electròlisi una fina capa d’aïllant. Degut al procés de fabricació tenen una polaritat que cal respectar; en cas contrari el condensador es curtcircuita i pot explotar.

També hi ha condensadors variables. Els condensadors variables consten d’un grup d’armadures que poden girar sobre un eix, de manera que la superfície enfrentada a l’armadura fixe sigui variable. El dielectric pot ser aire o bé làmines de plàstic o de mica.

Finalment, cal considerar els condensadors ajustables: s’anomenen vulgarment trimmers. El dielèctric també pot ser de aire, mica i ceràmics. Són més petits que els variables i s’ajusten amb l’ajut d’un tornavís.

Temps de Càrrega i Descàrrega d’un Condensador

Els temps que un condensador triga en carregar-se qual se’l sotmet a un determinat voltatge V₀ constant depèn de la capacitat del condensador i de la resistència a través de la qual es carrega el condensador. Suposem doncs un circuit constituit per una font de tensió de voltatge V₀ que amb la que es vol carregar un condensador de capacitat C a través d’una resistència R. Suposem que connectem el circuit a t=0 i que q(t=0)=0. Per deduir que passa escribim la llei de Kirchhof:

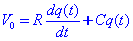
La solució d’aquesta equació és immediata:

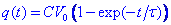
on la constant de temps τ = RC.  Per aquest temps el condensador carrega aprox. El 63% de la càrrega màxima. Es considera que un condensador està carregat quan τ supera el temps T = 3RC (95% de la càrrega màxima). Un cop carregat podem considerar ara la descàrrega d’un condensador sobre una resistència R. Tindrem aleshores que resoldre l’equació:

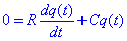
amb la condició q(t=0) = V₀/C. Aleshores es resol immediatament:

La representació gràfica de la càrrega i descàrrega d'un condensador estè representada en els gràfics següents:

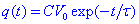
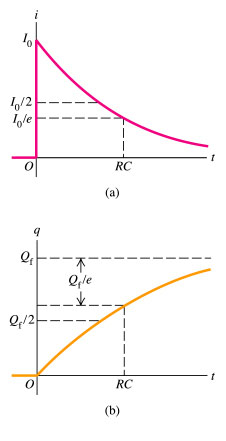
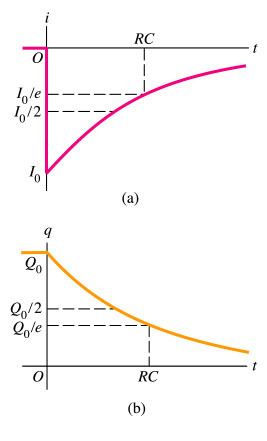
Energia acumulada en un condensador

Anem a calcular ara l’energia que acumula un condensador de capacitat C quan se’l carrega fins a un cert voltatge V₀. L’energia necessaria per afegir una certa quantitat de càrrega Δq a una tensió V és ΔU=ΔqV. Per tant l’energia acumulada és:

Les Inductàncies

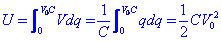
Constitució i característiques bàsiques de les inductàncies

Anomenem inductància a un element de circuit que genera un cert flux de camp magnetic quan es travessat per un corrent elèctric. Les equacions de Maxwell ens diuen que una variació d’aquest flux de camp magnètic genera una cert fem a l’inductància. Anem a veure-ho.

Considerem la segona equació de Maxwell i utilitzant el teorema de Stockes l’escrivim en forma integral:

 

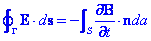
on Γ es qualsevol corba tancada i S és qualsevol superfície delimitada per la corba. Queda clar que Γ és una corba fixa i S és una superfície fixa. En aquest cas podem escriure:

 

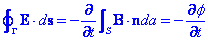
Per tant escrivim la fem ε com:

 

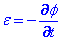
Utlitzant aquesta llei bàsica podem determinar les propietats elèctriques d’una inductància.

Si considerem un únic solenoide, sense nucli, en el que el corrent varia, també varia el propi flux de camp magnètic que crea el propi solenoide, i aquesta variació produirà el que anomenem una autoinductància o fem. Aquesta fem serà proporcional a la variació del corrent del propi solenoide:

 

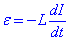
El signe menys significa que aquesta fem s’oposa al canvi de corrent

Podem calcular el valor de la inductància L fàcilment. El flux de camp magnètic en un solenoide es pot escriure com:

 

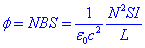
per tant per a un solenoide:

 

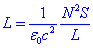
La constant s’anomena permeabilitat magnètica del buit. Quan s’hi afegeix un nucli d’acer o de ferrita aleshores la inductància resultant és la del buit multiplicada per un factor anomenat permeabilitat relativa que és característic de cada material. Tant l’acer com la ferrita tenen permeabilitats relatives elevades.

Tipus d’inductàncies

Generalment acostumen a ésser bobinats amb o sense nucli, d’una o varies capes i amb el nucli tancat o obert. També hi ha bobines planes en forma d’espiral que s’utilitzen per altes freqüències (microones).

Les característiques del nucli del bobinat depenen molt de la freqüència de treball. Per baixes freqüències es poden utilitzar nuclis constituits per xapes d’acer aïllades entre si, com es fa per exemple, en els motors i en els transformadors. A freqüències més elevades, com per exemple en radiofreqüència, s’utilitzen nuclis de ferrita, que no són conductores de l’electricitat però posseixen una permeabilitat magnètica relativament elevada, però no tant com l’acer. Amb nuclis tancats s’aconsegueixen fluxos de camp magnètic més elevats que amb nucli oberts.

Inèrcia elèctrica de les bobines

Quan en un circuit de corrent continu, hi ha inductàncies (com és el cas d’un electroiman), la intensitat de corrent pot presentar una forta depèndencia amb el temps. A més, veurem que si intentem desconnectar un circuit de CC, haurem de prendre preucacions. Suposem doncs un circuit constituit per una font de tensió de voltatge V₀ que amb la s’alimenta una inductància L a través d’una resistència R. Suposem que connectem el circuit a t=0. Per deduir que passa escribim la llei de Kirchhof:

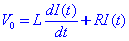
Aquesta equació es resol ràpidament:

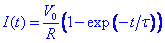
on τ = L/R s’anomena constant de temps i ens indica quan de temps ha de passar per a que la intensitat de corrent arribi al 63% del seu valor màxim. Es considera que s’ha arribat a la intensitat màxima per T=5τ (99% de la intensitat). Com que les inductàncies grans acostumen a tenir una certa resistència (degut a la longitud dels conductors del bobinats) els temps per arribar al valor màxim pot ser no menyspreable.

Una vegada establert el corrent cal anar en compte quan es vol desconnectar el circuit. Si desconnectessim bruscament, es produiria una fem a la inductància que és prporcional a la variació de la intensitat. Per tant fàcliment les inductàncies poden generar fems de milers de volts en aquestes situacions (aquest fet té aplicacions pràctiques, en fluorescents, en els cotxes amb motor de benzina, etc). Per evitar sobretensions, el que és fa es connectar una resistència en paral·lel a la bobina en el moment de la desconnexió, perquè d’aquesta manera l’energia acumulada a la bobina es consumeixi en forma de calor a la resistència.

Per a calcular el temps necessari per a que això passi, haurem de resoldre l’equació:

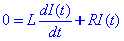
amb la condició I(t=0)=I₀.

La solució és immediata:

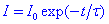
Energia acumulada en una inductància

La potència que consumeix la font per alimentar la bobina es pot escriure com:

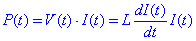
Integrant respecte del temps:

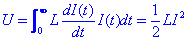
En els motors i en els transformadors es poden arribar a acumular energies molt grans.

Comportament de resistències bobines i condensadors en circuits de corrent altern.

Circuit LCR

Per tal d’esbrinar el comportament de les resistències, els condensadors i les inductàncies en els circuits de corrent alterna, comencem considerant una situació relativament simple: suposem un circuit LCR en el que trobem una resistència, un condensador i una inductància connectats en sèrie entre si i amb un generador de corrent altern. La suma de caigudes de tensió a cada element haurà de ser igual al voltatge del generador, i per tant:

Aquesta equació és la mateixa d’un oscil·lador harmònic forçat. Si pensem que la càrrega q en un condensador és anàleg al desplaçament x, veiem que el corrent és anàleg a la velocitat, 1/C és anàleg a la constant k de la molla i R és anàleg al coeficient de fricció. El coeficient L és anàleg a la massa. Suposarem que V(t) oscil·la harmònicament en el temps. Com que l’equació que hem de resoldre és linial, resulta molt adient definir un voltatge complex . 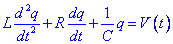La part real d’aquest voltatge es correspondrà amb el voltatge que genera el generador. També fem el mateix amb la càrrega i escribim . Substituint a l’equació diferencial obtenim:

o bé:

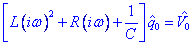
Podem calcular la intensitat derivant la càrrega respecte del temps:

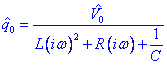
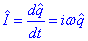
Si escribim obtenim:

definim aleshores el que anomenem una impedància complexe Z:

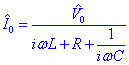
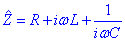
Per tant la llei d’Ohm l’escriurem a partir d’ara com . Aquesta expressió de la impedància clarament correspon a la suma de les impedàncies de cadescun dels elements que hi ha en el circuit. Podem escriure aleshores:

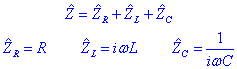
El fet que Z sigui un numero complex té una implicació molt important: implica un cert defassatge entre el potencial i la intensitat. En el nostre circuit Z es pot escriure com:

  Per tant la intensitat es pot escriure finalment com:

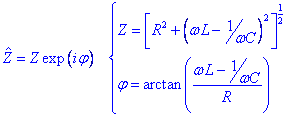
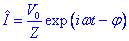
Utilizant la llei d’Ohm, resulta possible a més calcular les caigudes de tensió a cadescún dels elements del circuit. Els resultat per a un circuit inductiu correspon al cas b) mentre que el cas c) correspon a un circuit capacitiu.


24.2.2 Anàlisi d’un circuit arbitrari.

Un circuït arbitrari es caracteritza per la seva impedància complexe Z. La resolució d’un circuit en corrent altern és anàloga a la resolució de circuits en corrent continu i s’apliquen també les lleis de Kirchhoff, això si, treballant amb voltatges, intensitats i impedàncies complexes. Un cop calculada o mesurada la impedància d’un circuit, podem calcular la intensitat que el travessa utilitzant la llei d’Ohm, tal i com ho em fet en l’apartat anterior.


24.3 Potència en corrent altern

Suposem un cert aparell elèctric connectat a un generador de corrent altern. El voltatge i la intensitat que travessen l’aparell es podran escriure com:

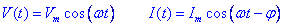
Utilitzant aquesta identitat: escribim:

El primer terme rep el nom d’intensitat activa I_a i el segon terme s’anomena intensitat reactiva I_r. La potència que consumeix l’aparell es pot escriure com:

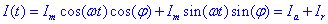
Ens interessa calcular la potència mitjana consumida per l’aparell, és a dir:

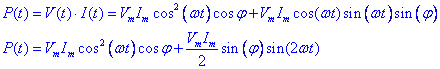
Fixem-nos en que en l’expressió de P(t) tenim un primer terme que tindrà un promig temporal diferent de zero i un segon terme de promig zero. Per tant:

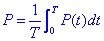
D’aquesta potència que consumeix l’aparell en diem potència activa i es mesura en Watts. Aquesta potència pot apareixer en forma de calor, potència mecànica, etc. Anem a analitzar ara el terme que té promig zero. L’existència d’aquesta terme implica que hi ha una part de potència que el generador proporciona a l’aparell durant un cert temps T/4 i l’aparell la retorna durant un periode de temps T/4. Aquesta energia no es consumeix i correspon a l’energia que periòdicament s’emmagatzema temporalment en els condensadors i a les inductàncies i periòdicament es retorna al generador. Es defineix aleshores la potència reactiva Q com:

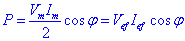
Aquesta potència es mesura en Volts · Ampers reactius (VAr). Finalment es defineix també la potència aparent S com:

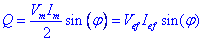
que es mesura en volt·ampère (VA). De la definició anterior: